|
SNAP Library 2.1, Developer Reference
2013-09-25 10:47:25
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
|
|
SNAP Library 2.1, Developer Reference
2013-09-25 10:47:25
SNAP, a general purpose, high performance system for analysis and manipulation of large networks
|
!!!!! MYUNGHWAN, CHECK! More...
#include <kronecker.h>

Public Member Functions | |
| TKroneckerLL () | |
| TKroneckerLL (const PNGraph &GraphPt, const TFltV &ParamV, const double &PermPSwapNd=0.2) | |
| TKroneckerLL (const PNGraph &GraphPt, const TKronMtx &ParamMtx, const double &PermPSwapNd=0.2) | |
| TKroneckerLL (const PNGraph &GraphPt, const TKronMtx &ParamMtx, const TIntV &NodeIdPermV, const double &PermPSwapNd=0.2) | |
| int | GetNodes () const |
| int | GetKronIters () const |
| PNGraph | GetGraph () const |
| void | SetGraph (const PNGraph &GraphPt) |
| const TKronMtx & | GetProbMtx () const |
| const TKronMtx & | GetLLMtx () const |
| int | GetParams () const |
| int | GetDim () const |
| void | SetDebug (const bool Debug) |
| const TFltV & | GetLLHist () const |
| const TVec< TKronMtx > & | GetParamHist () const |
| bool | IsObsNode (const int &NId) const |
| bool | IsObsEdge (const int &NId1, const int &NId2) const |
| bool | IsLatentNode (const int &NId) const |
| bool | IsLatentEdge (const int &NId1, const int &NId2) const |
| void | SetPerm (const char &PermId) |
| void | SetOrderPerm () |
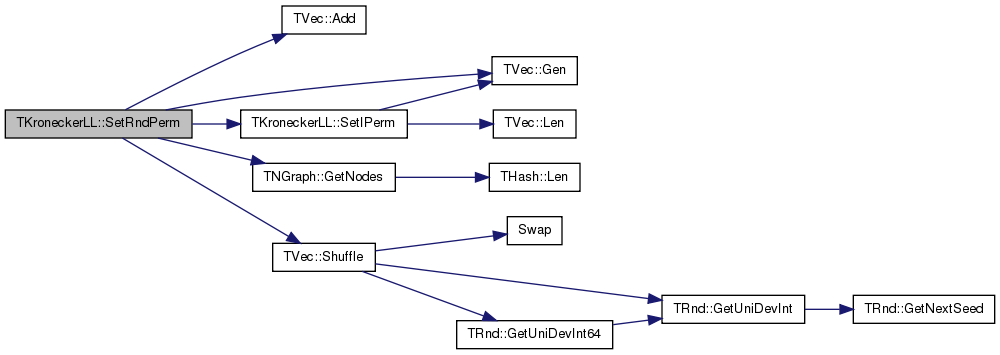
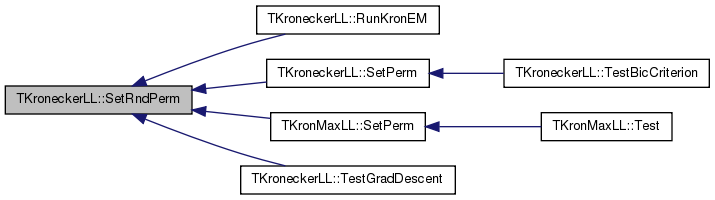
| void | SetRndPerm () |
| void | SetDegPerm () |
| void | SetBestDegPerm () |
| !!!!! MYUNGHWAN, CHECK! | |
| void | SetPerm (const TIntV &NodePermV) |
| void | SetIPerm (const TIntV &Perm) |
| !!!!! MYUNGHWAN, CHECK! | |
| const TIntV & | GetPermV () const |
| void | AppendIsoNodes () |
| void | RestoreGraph (const bool RestoreNodes=true) |
| !!!!! MYUNGHWAN, CHECK! | |
| double | GetFullGraphLL () const |
| double | GetFullRowLL (int RowId) const |
| double | GetFullColLL (int ColId) const |
| double | GetEmptyGraphLL () const |
| double | GetApxEmptyGraphLL () const |
| void | InitLL (const TFltV &ParamV) |
| void | InitLL (const TKronMtx &ParamMtx) |
| void | InitLL (const PNGraph &GraphPt, const TKronMtx &ParamMtx) |
| double | CalcGraphLL () |
| double | CalcApxGraphLL () |
| double | GetLL () const |
| double | GetAbsErr () const |
| double | NodeLLDelta (const int &NId) const |
| double | SwapNodesLL (const int &NId1, const int &NId2) |
| bool | SampleNextPerm (int &NId1, int &NId2) |
| double | GetEmptyGraphDLL (const int &ParamId) const |
| double | GetApxEmptyGraphDLL (const int &ParamId) const |
| const TFltV & | CalcGraphDLL () |
| const TFltV & | CalcFullApxGraphDLL () |
| const TFltV & | CalcApxGraphDLL () |
| double | NodeDLLDelta (const int ParamId, const int &NId) const |
| void | UpdateGraphDLL (const int &SwapNId1, const int &SwapNId2) |
| const TFltV & | GetDLL () const |
| double | GetDLL (const int &ParamId) const |
| void | SampleGradient (const int &WarmUp, const int &NSamples, double &AvgLL, TFltV &GradV) |
| double | GradDescent (const int &NIter, const double &LrnRate, double MnStep, double MxStep, const int &WarmUp, const int &NSamples) |
| double | GradDescent2 (const int &NIter, const double &LrnRate, double MnStep, double MxStep, const int &WarmUp, const int &NSamples) |
| void | SetRandomEdges (const int &NEdges, const bool isDir=true) |
| !!!!! MYUNGHWAN, CHECK! | |
| void | MetroGibbsSampleSetup (const int &WarmUp) |
| void | MetroGibbsSampleNext (const int &WarmUp, const bool DLLUpdate=false) |
| void | RunEStep (const int &GibbsWarmUp, const int &WarmUp, const int &NSamples, TFltV &LLV, TVec< TFltV > &DLLV) |
| double | RunMStep (const TFltV &LLV, const TVec< TFltV > &DLLV, const int &GradIter, const double &LrnRate, double MnStep, double MxStep) |
| void | RunKronEM (const int &EMIter, const int &GradIter, double LrnRate, double MnStep, double MxStep, const int &GibbsWarmUp, const int &WarmUp, const int &NSamples, const TKronEMType &Type=kronNodeMiss, const int &NMissing=-1) |
| TFltV | TestSamplePerm (const TStr &OutFNm, const int &WarmUp, const int &NSamples, const TKronMtx &TrueMtx, const bool &DoPlot=true) |
| TFltQu | TestKronDescent (const bool &DoExact, const bool &TruePerm, double LearnRate, const int &WarmUp, const int &NSamples, const TKronMtx &TrueParam) |
| void | GradDescentConvergence (const TStr &OutFNm, const TStr &Desc1, const bool &SamplePerm, const int &NIters, double LearnRate, const int &WarmUp, const int &NSamples, const int &AvgKGraphs, const TKronMtx &TrueParam) |
Static Public Member Functions | |
| static PKroneckerLL | New () |
| static PKroneckerLL | New (const PNGraph &GraphPt, const TKronMtx &ParamMtx, const double &PermPSwapNd=0.1) |
| static PKroneckerLL | New (const PNGraph &GraphPt, const TKronMtx &ParamMtx, const TIntV &NodeIdPermV, const double &PermPSwapNd=0.2) |
| static double | CalcChainR2 (const TVec< TFltV > &ChainLLV) |
| static void | ChainGelmapRubinPlot (const TVec< TFltV > &ChainLLV, const TStr &OutFNm, const TStr &Desc) |
| static void | TestBicCriterion (const TStr &OutFNm, const TStr &Desc1, const PNGraph &G, const int &GradIters, double LearnRate, const int &WarmUp, const int &NSamples, const int &TrueN0) |
| static void | TestGradDescent (const int &KronIters, const int &KiloSamples, const TStr &Permutation) |
Private Attributes | |
| TCRef | CRef |
| PNGraph | Graph |
| TInt | Nodes |
| TInt | KronIters |
| TFlt | PermSwapNodeProb |
| TIntTrV | GEdgeV |
| TIntTrV | LEdgeV |
| TInt | LSelfEdge |
| TIntV | NodePerm |
| TIntV | InvertPerm |
| TInt | RealNodes |
| TInt | RealEdges |
| TKronMtx | ProbMtx |
| TKronMtx | LLMtx |
| TFlt | LogLike |
| TFltV | GradV |
| TKronEMType | EMType |
| TInt | MissEdges |
| TBool | DebugMode |
| TFltV | LLV |
| TVec< TKronMtx > | MtxV |
Friends | |
| class | TPt< TKroneckerLL > |
!!!!! MYUNGHWAN, CHECK!
Definition at line 116 of file kronecker.h.
| TKroneckerLL::TKroneckerLL | ( | ) | [inline] |
Definition at line 150 of file kronecker.h.
Referenced by New().
: Nodes(-1), KronIters(-1), PermSwapNodeProb(0.2), RealNodes(-1), RealEdges(-1), LogLike(TKronMtx::NInf), EMType(kronNodeMiss), MissEdges(-1), DebugMode(false) { }

| TKroneckerLL::TKroneckerLL | ( | const PNGraph & | GraphPt, |
| const TFltV & | ParamV, | ||
| const double & | PermPSwapNd = 0.2 |
||
| ) |
Definition at line 783 of file kronecker.cpp.
References InitLL().
: PermSwapNodeProb(PermPSwapNd) { InitLL(GraphPt, TKronMtx(ParamV)); }

| TKroneckerLL::TKroneckerLL | ( | const PNGraph & | GraphPt, |
| const TKronMtx & | ParamMtx, | ||
| const double & | PermPSwapNd = 0.2 |
||
| ) |
Definition at line 787 of file kronecker.cpp.
References InitLL().
: PermSwapNodeProb(PermPSwapNd) { InitLL(GraphPt, ParamMtx); }

| TKroneckerLL::TKroneckerLL | ( | const PNGraph & | GraphPt, |
| const TKronMtx & | ParamMtx, | ||
| const TIntV & | NodeIdPermV, | ||
| const double & | PermPSwapNd = 0.2 |
||
| ) |
Definition at line 791 of file kronecker.cpp.
References InitLL(), NodePerm, and SetIPerm().
: PermSwapNodeProb(PermPSwapNd) { InitLL(GraphPt, ParamMtx); NodePerm = NodeIdPermV; SetIPerm(NodePerm); }
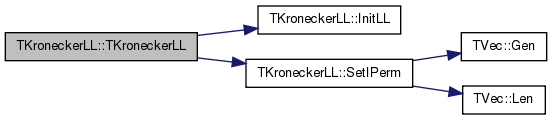
| void TKroneckerLL::AppendIsoNodes | ( | ) |
Definition at line 914 of file kronecker.cpp.
References TNGraph::AddNode(), TKronMtx::GetDim(), TNGraph::GetNodes(), Graph, KronIters, Nodes, and ProbMtx.
Referenced by RunKronEM().
{
Nodes = (int) pow((double)ProbMtx.GetDim(), KronIters);
// add nodes until filling the Kronecker graph model
for (int nid = Graph->GetNodes(); nid < Nodes; nid++) {
Graph->AddNode(nid);
}
}
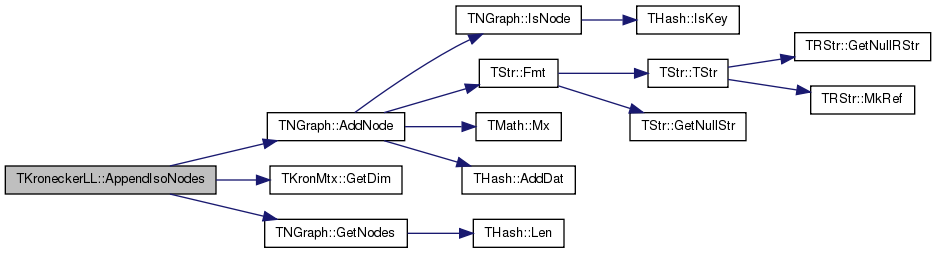

| const TFltV & TKroneckerLL::CalcApxGraphDLL | ( | ) |
Definition at line 1194 of file kronecker.cpp.
References GetApxEmptyGraphDLL(), TKronMtx::GetApxNoEdgeDLL(), TKronMtx::GetEdgeDLL(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), GradV, Graph, KronIters, TKronMtx::Len(), LLMtx, NodePerm, and Nodes.
Referenced by GradDescentConvergence(), RunEStep(), RunMStep(), SampleGradient(), TestGradDescent(), TestKronDescent(), and TestSamplePerm().
{
for (int ParamId = 0; ParamId < LLMtx.Len(); ParamId++) {
double DLL = GetApxEmptyGraphDLL(ParamId);
for (int nid = 0; nid < Nodes; nid++) {
const TNGraph::TNodeI Node = Graph->GetNI(nid);
const int SrcNId = NodePerm[nid];
for (int e = 0; e < Node.GetOutDeg(); e++) {
const int DstNId = NodePerm[Node.GetOutNId(e)];
DLL = DLL - LLMtx.GetApxNoEdgeDLL(ParamId, SrcNId, DstNId, KronIters)
+ LLMtx.GetEdgeDLL(ParamId, SrcNId, DstNId, KronIters);
}
}
GradV[ParamId] = DLL;
}
return GradV;
}
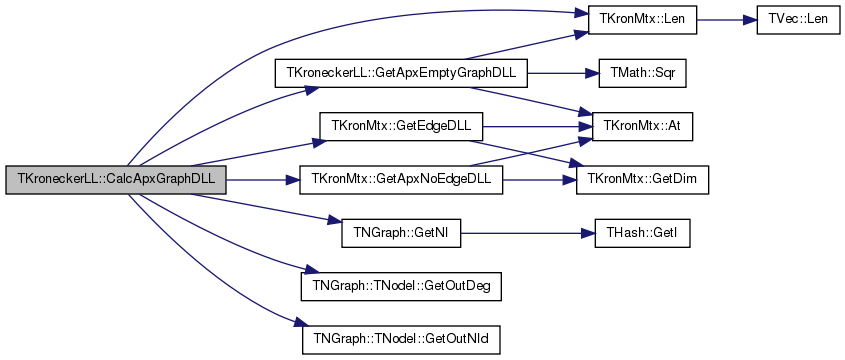
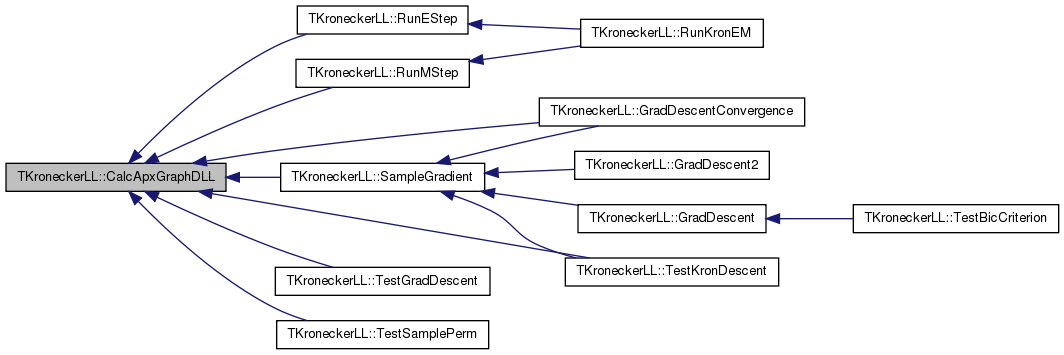
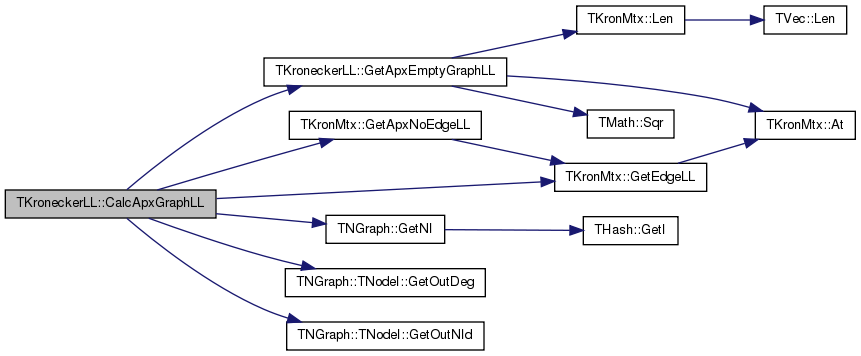
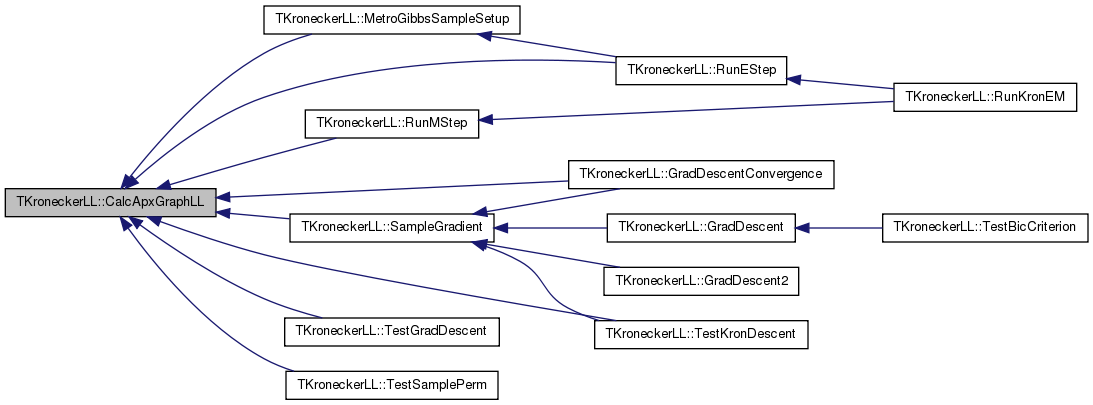
| double TKroneckerLL::CalcApxGraphLL | ( | ) |
Definition at line 1037 of file kronecker.cpp.
References GetApxEmptyGraphLL(), TKronMtx::GetApxNoEdgeLL(), TKronMtx::GetEdgeLL(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), Graph, KronIters, LLMtx, LogLike, NodePerm, and Nodes.
Referenced by GradDescentConvergence(), MetroGibbsSampleSetup(), RunEStep(), RunMStep(), SampleGradient(), TestGradDescent(), TestKronDescent(), and TestSamplePerm().
{
LogLike = GetApxEmptyGraphLL(); // O(N_0)
for (int nid = 0; nid < Nodes; nid++) {
const TNGraph::TNodeI Node = Graph->GetNI(nid);
const int SrcNId = NodePerm[nid];
for (int e = 0; e < Node.GetOutDeg(); e++) {
const int DstNId = NodePerm[Node.GetOutNId(e)];
LogLike = LogLike - LLMtx.GetApxNoEdgeLL(SrcNId, DstNId, KronIters)
+ LLMtx.GetEdgeLL(SrcNId, DstNId, KronIters);
}
}
return LogLike;
}
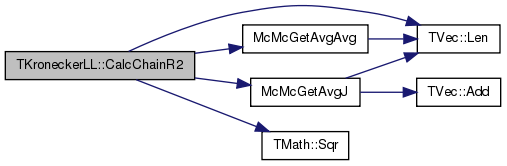
| double TKroneckerLL::CalcChainR2 | ( | const TVec< TFltV > & | ChainLLV | ) | [static] |
Definition at line 1895 of file kronecker.cpp.
References IAssert, TVec< TVal, TSizeTy >::Len(), McMcGetAvgAvg(), McMcGetAvgJ(), and TMath::Sqr().
Referenced by ChainGelmapRubinPlot().
{
const double J = ChainLLV.Len();
const double K = ChainLLV[0].Len();
TFltV AvgJV; McMcGetAvgJ(ChainLLV, AvgJV);
double AvgAvg; McMcGetAvgAvg(AvgJV, AvgAvg);
IAssert(AvgJV.Len() == ChainLLV.Len());
double InChainVar=0, OutChainVar=0;
// between chain var
for (int j = 0; j < AvgJV.Len(); j++) {
OutChainVar += TMath::Sqr(AvgJV[j] - AvgAvg); }
OutChainVar = OutChainVar * (K/double(J-1));
printf("*** %g chains of len %g\n", J, K);
printf(" ** between chain var: %f\n", OutChainVar);
//within chain variance
for (int j = 0; j < AvgJV.Len(); j++) {
const TFltV& ChainV = ChainLLV[j];
for (int k = 0; k < ChainV.Len(); k++) {
InChainVar += TMath::Sqr(ChainV[k] - AvgJV[j]); }
}
InChainVar = InChainVar * 1.0/double(J*(K-1));
printf(" ** within chain var: %f\n", InChainVar);
const double PostVar = (K-1)/K * InChainVar + 1.0/K * OutChainVar;
printf(" ** posterior var: %f\n", PostVar);
const double ScaleRed = sqrt(PostVar/InChainVar);
printf(" ** scale reduction (< 1.2): %f\n\n", ScaleRed);
return ScaleRed;
}

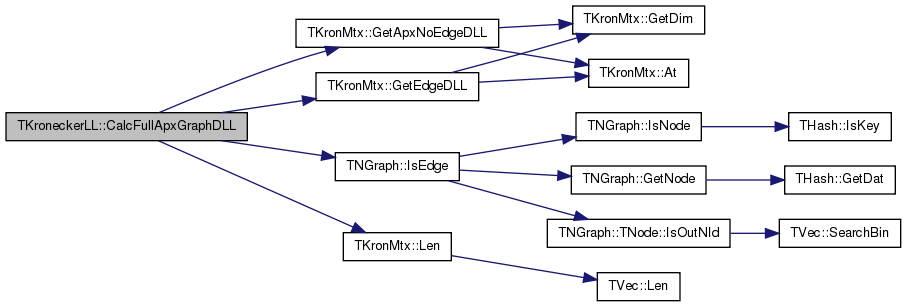
| const TFltV & TKroneckerLL::CalcFullApxGraphDLL | ( | ) |
Definition at line 1176 of file kronecker.cpp.
References TKronMtx::GetApxNoEdgeDLL(), TKronMtx::GetEdgeDLL(), GradV, Graph, TNGraph::IsEdge(), KronIters, TKronMtx::Len(), LLMtx, NodePerm, and Nodes.
{
for (int ParamId = 0; ParamId < LLMtx.Len(); ParamId++) {
double DLL = 0.0;
for (int NId1 = 0; NId1 < Nodes; NId1++) {
for (int NId2 = 0; NId2 < Nodes; NId2++) {
if (Graph->IsEdge(NId1, NId2)) {
DLL += LLMtx.GetEdgeDLL(ParamId, NodePerm[NId1], NodePerm[NId2], KronIters);
} else {
DLL += LLMtx.GetApxNoEdgeDLL(ParamId, NodePerm[NId1], NodePerm[NId2], KronIters);
}
}
}
GradV[ParamId] = DLL;
}
return GradV;
}
| const TFltV & TKroneckerLL::CalcGraphDLL | ( | ) |
Definition at line 1158 of file kronecker.cpp.
References TKronMtx::GetEdgeDLL(), TKronMtx::GetNoEdgeDLL(), GradV, Graph, TNGraph::IsEdge(), KronIters, TKronMtx::Len(), LLMtx, NodePerm, and Nodes.
Referenced by TestKronDescent().
{
for (int ParamId = 0; ParamId < LLMtx.Len(); ParamId++) {
double DLL = 0.0;
for (int NId1 = 0; NId1 < Nodes; NId1++) {
for (int NId2 = 0; NId2 < Nodes; NId2++) {
if (Graph->IsEdge(NId1, NId2)) {
DLL += LLMtx.GetEdgeDLL(ParamId, NodePerm[NId1], NodePerm[NId2], KronIters);
} else {
DLL += LLMtx.GetNoEdgeDLL(ParamId, NodePerm[NId1], NodePerm[NId2], KronIters);
}
}
}
GradV[ParamId] = DLL;
}
return GradV;
}

| double TKroneckerLL::CalcGraphLL | ( | ) |
Definition at line 1022 of file kronecker.cpp.
References TKronMtx::GetEdgeLL(), GetEmptyGraphLL(), TNGraph::GetNI(), TKronMtx::GetNoEdgeLL(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), Graph, KronIters, LLMtx, LogLike, NodePerm, and Nodes.
Referenced by TestKronDescent().
{
LogLike = GetEmptyGraphLL(); // takes O(N^2)
for (int nid = 0; nid < Nodes; nid++) {
const TNGraph::TNodeI Node = Graph->GetNI(nid);
const int SrcNId = NodePerm[nid];
for (int e = 0; e < Node.GetOutDeg(); e++) {
const int DstNId = NodePerm[Node.GetOutNId(e)];
LogLike = LogLike - LLMtx.GetNoEdgeLL(SrcNId, DstNId, KronIters)
+ LLMtx.GetEdgeLL(SrcNId, DstNId, KronIters);
}
}
return LogLike;
}

| void TKroneckerLL::ChainGelmapRubinPlot | ( | const TVec< TFltV > & | ChainLLV, |
| const TStr & | OutFNm, | ||
| const TStr & | Desc | ||
| ) | [static] |
Definition at line 1924 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), CalcChainR2(), TStr::CStr(), TStr::Fmt(), TVec< TVal, TSizeTy >::GetSubValV(), TVec< TVal, TSizeTy >::Len(), TMath::Mn(), and TGnuPlot::PlotValV().
{
TFltPrV LenR2V; // how does potential scale reduction chainge with chain length
TVec<TFltV> SmallLLV(ChainLLV.Len());
const int K = ChainLLV[0].Len();
const int Buckets=1000;
const int BucketSz = K/Buckets;
for (int b = 1; b < Buckets; b++) {
const int End = TMath::Mn(BucketSz*b, K-1);
for (int c = 0; c < ChainLLV.Len(); c++) {
ChainLLV[c].GetSubValV(0, End, SmallLLV[c]); }
LenR2V.Add(TFltPr(End, TKroneckerLL::CalcChainR2(SmallLLV)));
}
LenR2V.Add(TFltPr(K, TKroneckerLL::CalcChainR2(ChainLLV)));
TGnuPlot::PlotValV(LenR2V, TStr::Fmt("gelman-%s", OutFNm.CStr()), TStr::Fmt("%s. %d chains of len %d. BucketSz: %d.",
Desc.CStr(), ChainLLV.Len(), ChainLLV[0].Len(), BucketSz), "Chain length", "Potential scale reduction");
}
| double TKroneckerLL::GetAbsErr | ( | ) | const [inline] |
Definition at line 205 of file kronecker.h.
References TNGraph::GetEdges(), TKronMtx::GetMtxSum(), Graph, KronIters, and ProbMtx.
| double TKroneckerLL::GetApxEmptyGraphDLL | ( | const int & | ParamId | ) | const |
Definition at line 1147 of file kronecker.cpp.
References TKronMtx::At(), KronIters, TKronMtx::Len(), ProbMtx, and TMath::Sqr().
Referenced by CalcApxGraphDLL().
{
double Sum=0.0, SumSq=0.0;
for (int i = 0; i < ProbMtx.Len(); i++) {
Sum += ProbMtx.At(i);
SumSq += TMath::Sqr(ProbMtx.At(i));
}
// d/dx -sum(x_i) - 0.5sum(x_i^2) = d/dx sum(theta)^k - 0.5 sum(theta^2)^k
return -KronIters*pow(Sum, KronIters-1) - KronIters*pow(SumSq, KronIters-1)*ProbMtx.At(ParamId);
}

| double TKroneckerLL::GetApxEmptyGraphLL | ( | ) | const |
Definition at line 987 of file kronecker.cpp.
References TKronMtx::At(), KronIters, TKronMtx::Len(), ProbMtx, and TMath::Sqr().
Referenced by CalcApxGraphLL().
{
double Sum=0.0, SumSq=0.0;
for (int i = 0; i < ProbMtx.Len(); i++) {
Sum += ProbMtx.At(i);
SumSq += TMath::Sqr(ProbMtx.At(i));
}
return -pow(Sum, KronIters) - 0.5*pow(SumSq, KronIters);
}
| int TKroneckerLL::GetDim | ( | ) | const [inline] |
Definition at line 165 of file kronecker.h.
References TKronMtx::GetDim(), and ProbMtx.

| const TFltV& TKroneckerLL::GetDLL | ( | ) | const [inline] |
| double TKroneckerLL::GetDLL | ( | const int & | ParamId | ) | const [inline] |
| double TKroneckerLL::GetEmptyGraphDLL | ( | const int & | ParamId | ) | const |
Definition at line 1136 of file kronecker.cpp.
References TKronMtx::GetNoEdgeDLL(), KronIters, LLMtx, NodePerm, and Nodes.
{
double DLL = 0.0;
for (int NId1 = 0; NId1 < Nodes; NId1++) {
for (int NId2 = 0; NId2 < Nodes; NId2++) {
DLL += LLMtx.GetNoEdgeDLL(ParamId, NodePerm[NId1], NodePerm[NId2], KronIters);
}
}
return DLL;
}

| double TKroneckerLL::GetEmptyGraphLL | ( | ) | const |
Definition at line 976 of file kronecker.cpp.
References TKronMtx::GetNodes(), TKronMtx::GetNoEdgeLL(), KronIters, and LLMtx.
Referenced by CalcGraphLL().
{
double LL = 0;
for (int NId1 = 0; NId1 < LLMtx.GetNodes(KronIters); NId1++) {
for (int NId2 = 0; NId2 < LLMtx.GetNodes(KronIters); NId2++) {
LL = LL + LLMtx.GetNoEdgeLL(NId1, NId2, KronIters);
}
}
return LL;
}

| double TKroneckerLL::GetFullColLL | ( | int | ColId | ) | const |
Definition at line 966 of file kronecker.cpp.
References TKronMtx::GetColSum(), TKronMtx::GetDim(), KronIters, and LLMtx.
{
double ColLL = 0.0;
const int MtxDim = LLMtx.GetDim();
for (int level = 0; level < KronIters; level++) {
ColLL += LLMtx.GetColSum(ColId % MtxDim);
ColId /= MtxDim;
}
return ColLL;
}

| double TKroneckerLL::GetFullGraphLL | ( | ) | const |
Definition at line 943 of file kronecker.cpp.
References TKronMtx::GetDim(), TKronMtx::GetMtxSum(), KronIters, LLMtx, and TMath::Power().
{
// the number of times a seed matrix element appears in
// the full kronecker adjacency matrix after KronIter
// kronecker multiplications
double ElemCnt = 1;
const double dim = LLMtx.GetDim();
// count number of times x appears in the full kronecker matrix
for (int i = 1; i < KronIters; i++) {
ElemCnt = dim*dim*ElemCnt + TMath::Power(dim, 2*i);
}
return ElemCnt * LLMtx.GetMtxSum();
}
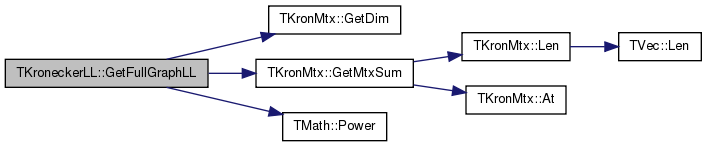
| double TKroneckerLL::GetFullRowLL | ( | int | RowId | ) | const |
Definition at line 956 of file kronecker.cpp.
References TKronMtx::GetDim(), TKronMtx::GetRowSum(), KronIters, and LLMtx.
{
double RowLL = 0.0;
const int MtxDim = LLMtx.GetDim();
for (int level = 0; level < KronIters; level++) {
RowLL += LLMtx.GetRowSum(RowId % MtxDim);
RowId /= MtxDim;
}
return RowLL;
}

| PNGraph TKroneckerLL::GetGraph | ( | ) | const [inline] |
| int TKroneckerLL::GetKronIters | ( | ) | const [inline] |
Definition at line 159 of file kronecker.h.
References KronIters.
Referenced by TestBicCriterion().
{ return KronIters; }

| double TKroneckerLL::GetLL | ( | ) | const [inline] |
Definition at line 204 of file kronecker.h.
References LogLike.
Referenced by SampleGradient(), and TestSamplePerm().
{ return LogLike; }

| const TFltV& TKroneckerLL::GetLLHist | ( | ) | const [inline] |
| const TKronMtx& TKroneckerLL::GetLLMtx | ( | ) | const [inline] |
| int TKroneckerLL::GetNodes | ( | ) | const [inline] |
| const TVec<TKronMtx>& TKroneckerLL::GetParamHist | ( | ) | const [inline] |
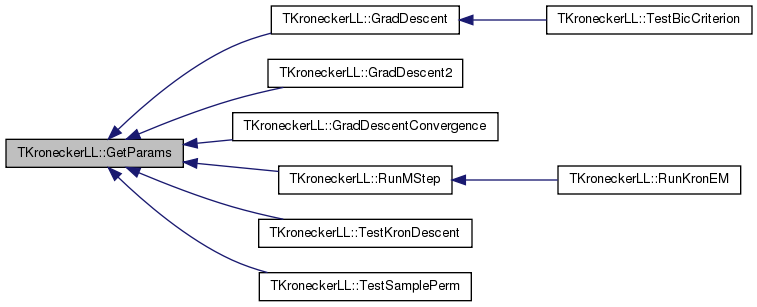
| int TKroneckerLL::GetParams | ( | ) | const [inline] |
Definition at line 164 of file kronecker.h.
References TKronMtx::Len(), and ProbMtx.
Referenced by GradDescent(), GradDescent2(), GradDescentConvergence(), RunMStep(), TestKronDescent(), and TestSamplePerm().

| const TIntV& TKroneckerLL::GetPermV | ( | ) | const [inline] |
| const TKronMtx& TKroneckerLL::GetProbMtx | ( | ) | const [inline] |
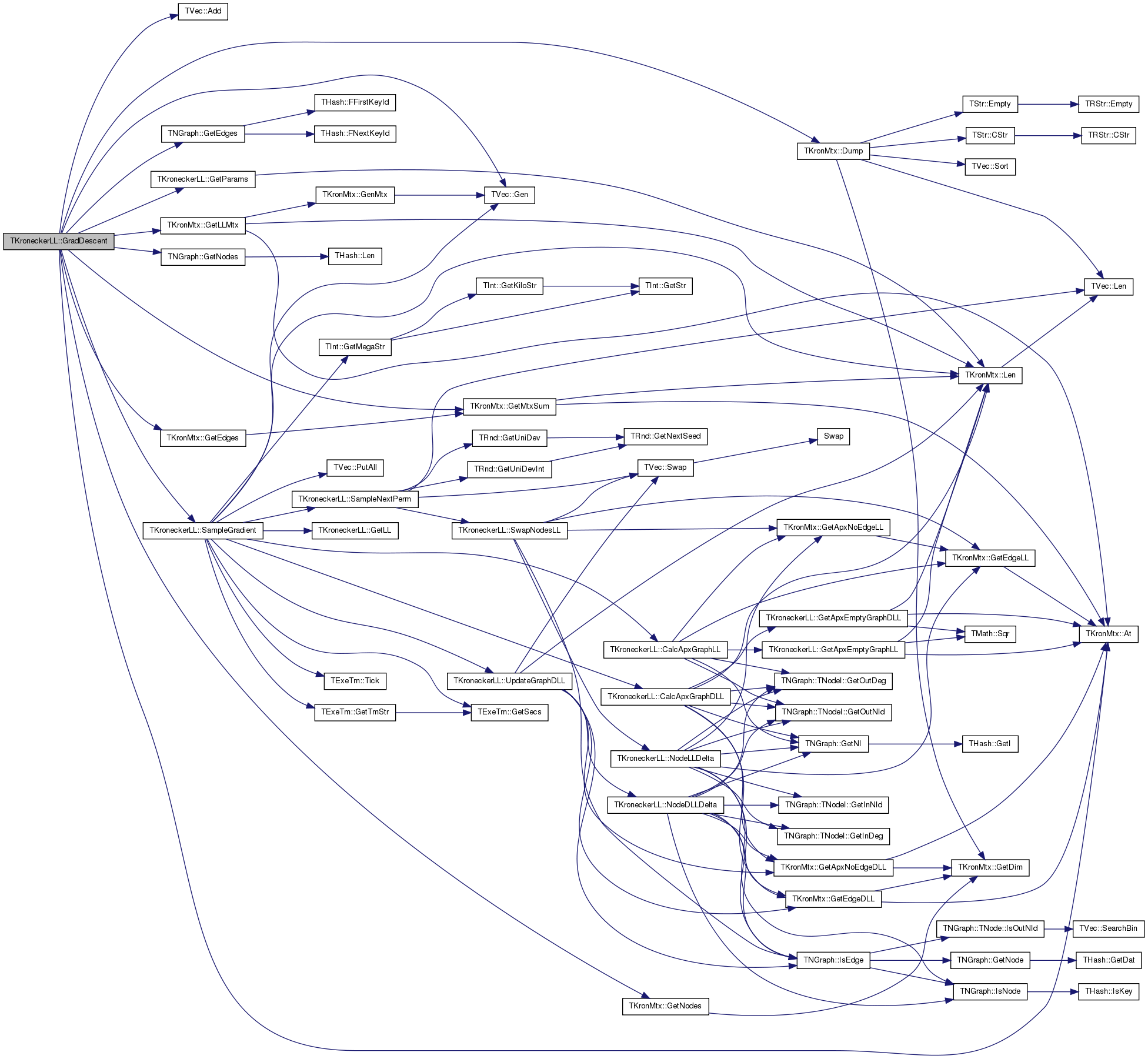
| double TKroneckerLL::GradDescent | ( | const int & | NIter, |
| const double & | LrnRate, | ||
| double | MnStep, | ||
| double | MxStep, | ||
| const int & | WarmUp, | ||
| const int & | NSamples | ||
| ) |
!!!!! MYUNGHWAN, CHECK!
!!!!! MYUNGHWAN, CHECK!
Definition at line 1299 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TKronMtx::At(), DebugMode, TKronMtx::Dump(), TVec< TVal, TSizeTy >::Gen(), TKronMtx::GetEdges(), TNGraph::GetEdges(), TKronMtx::GetLLMtx(), TKronMtx::GetMtxSum(), TKronMtx::GetNodes(), TNGraph::GetNodes(), GetParams(), Graph, KronIters, LLMtx, LLV, MtxV, ProbMtx, and SampleGradient().
Referenced by TestBicCriterion().
{
printf("\n----------------------------------------------------------------------\n");
printf("Fitting graph on %d nodes, %d edges\n", Graph->GetNodes(), Graph->GetEdges());
printf("Kron iters: %d (== %d nodes)\n\n", KronIters(), ProbMtx.GetNodes(KronIters()));
TExeTm IterTm, TotalTm;
double OldLL=-1e10, CurLL=0;
const double EZero = pow((double) Graph->GetEdges(), 1.0/double(KronIters));
TFltV CurGradV, LearnRateV(GetParams()), LastStep(GetParams());
LearnRateV.PutAll(LrnRate);
TKronMtx NewProbMtx = ProbMtx;
if(DebugMode) {
LLV.Gen(NIter, 0);
MtxV.Gen(NIter, 0);
}
for (int Iter = 0; Iter < NIter; Iter++) {
printf("%03d] ", Iter);
SampleGradient(WarmUp, NSamples, CurLL, CurGradV);
for (int p = 0; p < GetParams(); p++) {
LearnRateV[p] *= 0.95;
if (Iter < 1) {
while (fabs(LearnRateV[p]*CurGradV[p]) > MxStep) { LearnRateV[p] *= 0.95; }
while (fabs(LearnRateV[p]*CurGradV[p]) < 0.02) { LearnRateV[p] *= (1.0/0.95); } // move more
} else {
// set learn rate so that move for each parameter is inside the [MnStep, MxStep]
while (fabs(LearnRateV[p]*CurGradV[p]) > MxStep) { LearnRateV[p] *= 0.95; printf(".");}
while (fabs(LearnRateV[p]*CurGradV[p]) < MnStep) { LearnRateV[p] *= (1.0/0.95); printf("*");}
if (MxStep > 3*MnStep) { MxStep *= 0.95; }
}
NewProbMtx.At(p) = ProbMtx.At(p) + LearnRateV[p]*CurGradV[p];
if (NewProbMtx.At(p) > 0.9999) { NewProbMtx.At(p)=0.9999; }
if (NewProbMtx.At(p) < 0.0001) { NewProbMtx.At(p)=0.0001; }
}
printf(" trueE0: %.2f (%d), estE0: %.2f (%d), ERR: %f\n", EZero, Graph->GetEdges(),
ProbMtx.GetMtxSum(), ProbMtx.GetEdges(KronIters), fabs(EZero-ProbMtx.GetMtxSum()));
printf(" currLL: %.4f, deltaLL: %.4f\n", CurLL, CurLL-OldLL); // positive is good
for (int p = 0; p < GetParams(); p++) {
printf(" %d] %f <-- %f + %9f Grad: %9.1f Rate: %g\n", p, NewProbMtx.At(p),
ProbMtx.At(p), (double)(LearnRateV[p]*CurGradV[p]), CurGradV[p](), LearnRateV[p]());
}
if (Iter+1 < NIter) { // skip last update
ProbMtx = NewProbMtx; ProbMtx.GetLLMtx(LLMtx); }
OldLL=CurLL;
printf("\n"); fflush(stdout);
if(DebugMode) {
LLV.Add(CurLL);
MtxV.Add(NewProbMtx);
}
}
printf("TotalExeTm: %s %g\n", TotalTm.GetStr(), TotalTm.GetSecs());
ProbMtx.Dump("FITTED PARAMS", false);
return CurLL;
}

| double TKroneckerLL::GradDescent2 | ( | const int & | NIter, |
| const double & | LrnRate, | ||
| double | MnStep, | ||
| double | MxStep, | ||
| const int & | WarmUp, | ||
| const int & | NSamples | ||
| ) |
Definition at line 1355 of file kronecker.cpp.
References TKronMtx::At(), TKronMtx::Dump(), TKronMtx::GetEdges(), TNGraph::GetEdges(), TKronMtx::GetLLMtx(), TKronMtx::GetMtxSum(), TKronMtx::GetNodes(), TNGraph::GetNodes(), GetParams(), Graph, KronIters, LLMtx, ProbMtx, and SampleGradient().
{
printf("\n----------------------------------------------------------------------\n");
printf("GradDescent2\n");
printf("Fitting graph on %d nodes, %d edges\n", Graph->GetNodes(), Graph->GetEdges());
printf("Skip moves that make likelihood smaller\n");
printf("Kron iters: %d (== %d nodes)\n\n", KronIters(), ProbMtx.GetNodes(KronIters()));
TExeTm IterTm, TotalTm;
double CurLL=0, NewLL=0;
const double EZero = pow((double) Graph->GetEdges(), 1.0/double(KronIters));
TFltV CurGradV, NewGradV, LearnRateV(GetParams()), LastStep(GetParams());
LearnRateV.PutAll(LrnRate);
TKronMtx NewProbMtx=ProbMtx, CurProbMtx=ProbMtx;
bool GoodMove = false;
// Start
for (int Iter = 0; Iter < NIter; Iter++) {
printf("%03d] ", Iter);
if (! GoodMove) { SampleGradient(WarmUp, NSamples, CurLL, CurGradV); }
CurProbMtx = ProbMtx;
// update parameters
for (int p = 0; p < GetParams(); p++) {
while (fabs(LearnRateV[p]*CurGradV[p]) > MxStep) { LearnRateV[p] *= 0.95; printf(".");}
while (fabs(LearnRateV[p]*CurGradV[p]) < MnStep) { LearnRateV[p] *= (1.0/0.95); printf("*");}
NewProbMtx.At(p) = CurProbMtx.At(p) + LearnRateV[p]*CurGradV[p];
if (NewProbMtx.At(p) > 0.9999) { NewProbMtx.At(p)=0.9999; }
if (NewProbMtx.At(p) < 0.0001) { NewProbMtx.At(p)=0.0001; }
LearnRateV[p] *= 0.95;
}
printf(" ");
ProbMtx=NewProbMtx; ProbMtx.GetLLMtx(LLMtx);
SampleGradient(WarmUp, NSamples, NewLL, NewGradV);
if (NewLL > CurLL) { // accept the move
printf("== Good move:\n");
printf(" trueE0: %.2f (%d), estE0: %.2f (%d), ERR: %f\n", EZero, Graph->GetEdges(),
ProbMtx.GetMtxSum(), ProbMtx.GetEdges(KronIters), fabs(EZero-ProbMtx.GetMtxSum()));
printf(" currLL: %.4f deltaLL: %.4f\n", CurLL, NewLL-CurLL); // positive is good
for (int p = 0; p < GetParams(); p++) {
printf(" %d] %f <-- %f + %9f Grad: %9.1f Rate: %g\n", p, NewProbMtx.At(p),
CurProbMtx.At(p), (double)(LearnRateV[p]*CurGradV[p]), CurGradV[p](), LearnRateV[p]()); }
CurLL = NewLL;
CurGradV = NewGradV;
GoodMove = true;
} else {
printf("** BAD move:\n");
printf(" *trueE0: %.2f (%d), estE0: %.2f (%d), ERR: %f\n", EZero, Graph->GetEdges(),
ProbMtx.GetMtxSum(), ProbMtx.GetEdges(KronIters), fabs(EZero-ProbMtx.GetMtxSum()));
printf(" *curLL: %.4f deltaLL: %.4f\n", CurLL, NewLL-CurLL); // positive is good
for (int p = 0; p < GetParams(); p++) {
printf(" b%d] %f <-- %f + %9f Grad: %9.1f Rate: %g\n", p, NewProbMtx.At(p),
CurProbMtx.At(p), (double)(LearnRateV[p]*CurGradV[p]), CurGradV[p](), LearnRateV[p]()); }
// move to old position
ProbMtx = CurProbMtx; ProbMtx.GetLLMtx(LLMtx);
GoodMove = false;
}
printf("\n"); fflush(stdout);
}
printf("TotalExeTm: %s %g\n", TotalTm.GetStr(), TotalTm.GetSecs());
ProbMtx.Dump("FITTED PARAMS\n", false);
return CurLL;
}

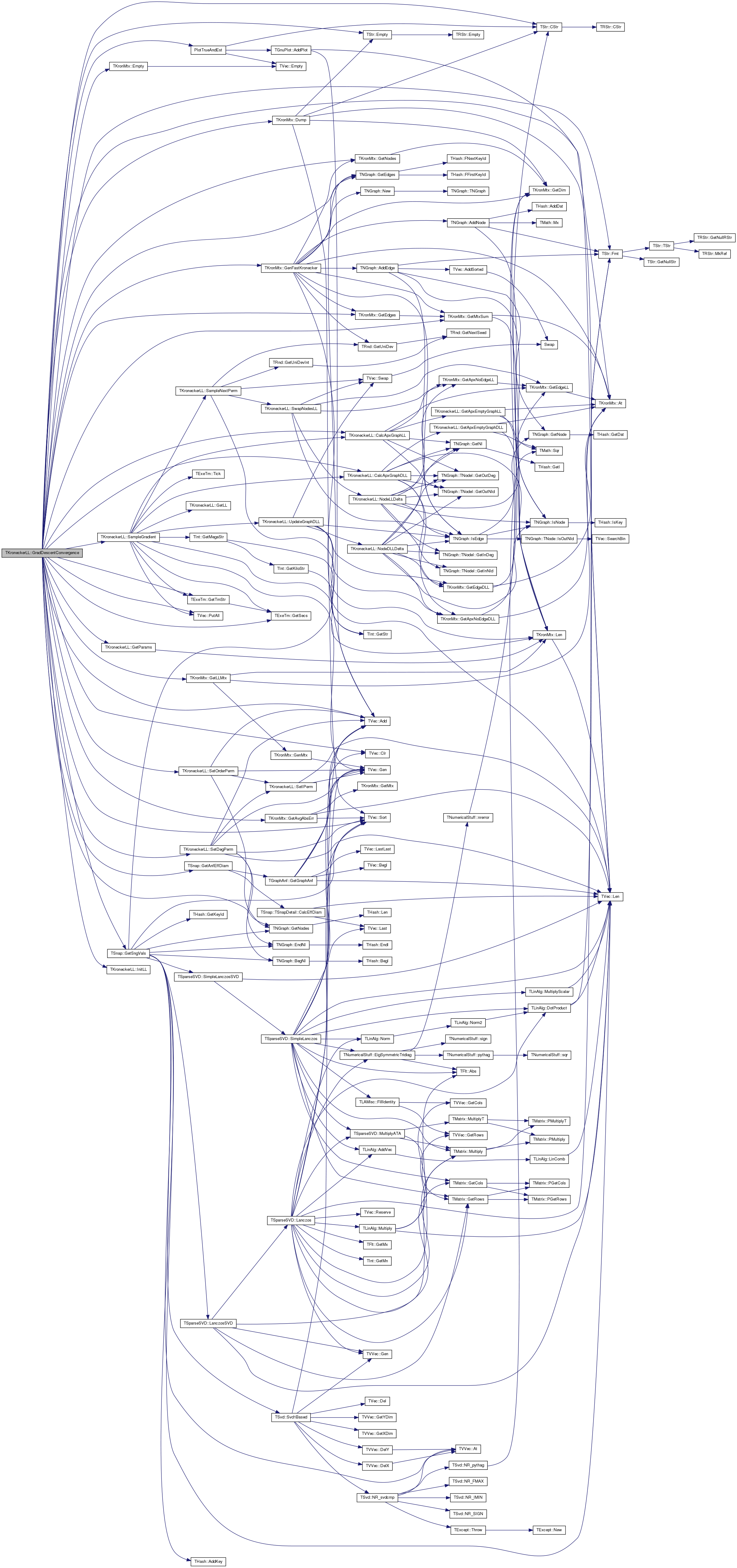
| void TKroneckerLL::GradDescentConvergence | ( | const TStr & | OutFNm, |
| const TStr & | Desc1, | ||
| const bool & | SamplePerm, | ||
| const int & | NIters, | ||
| double | LearnRate, | ||
| const int & | WarmUp, | ||
| const int & | NSamples, | ||
| const int & | AvgKGraphs, | ||
| const TKronMtx & | TrueParam | ||
| ) |
Definition at line 2017 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TKronMtx::At(), CalcApxGraphDLL(), CalcApxGraphLL(), TVec< TVal, TSizeTy >::Clr(), TStr::CStr(), TKronMtx::Dump(), TKronMtx::Empty(), TStr::Empty(), TStr::Fmt(), TKronMtx::GenFastKronecker(), TSnap::GetAnfEffDiam(), TKronMtx::GetAvgAbsErr(), TKronMtx::GetEdges(), TNGraph::GetEdges(), TKronMtx::GetLLMtx(), TKronMtx::GetMtxSum(), TKronMtx::GetNodes(), TNGraph::GetNodes(), GetParams(), TExeTm::GetSecs(), TSnap::GetSngVals(), TExeTm::GetTmStr(), GradV, Graph, InitLL(), KronIters, LLMtx, LogLike, PlotTrueAndEst(), ProbMtx, TVec< TVal, TSizeTy >::PutAll(), SampleGradient(), SetDegPerm(), SetOrderPerm(), and TVec< TVal, TSizeTy >::Sort().
{
TExeTm IterTm;
int Iter;
double OldLL=0, MyLL=0, AvgAbsErr=0, AbsSumErr=0;
TFltV MyGradV, SDevV;
TFltV LearnRateV(GetParams()); LearnRateV.PutAll(LearnRate);
TFltPrV EZeroV, DiamV, Lambda1V, Lambda2V, AvgAbsErrV, AvgLLV;
TFltPrV TrueEZeroV, TrueDiamV, TrueLambda1V, TrueLambda2V, TrueLLV;
TFltV SngValV; TSnap::GetSngVals(Graph, 2, SngValV); SngValV.Sort(false);
const double TrueEZero = pow((double) Graph->GetEdges(), 1.0/double(KronIters));
const double TrueEffDiam = TSnap::GetAnfEffDiam(Graph, false, 10);
const double TrueLambda1 = SngValV[0];
const double TrueLambda2 = SngValV[1];
if (! TrueParam.Empty()) {
const TKronMtx CurParam = ProbMtx; ProbMtx.Dump();
InitLL(TrueParam); SetOrderPerm(); CalcApxGraphLL(); printf("TrueLL: %f\n", LogLike());
OldLL = LogLike; InitLL(CurParam);
}
const double TrueLL = OldLL;
if (! SamplePerm) { SetOrderPerm(); } else { SetDegPerm(); }
for (Iter = 0; Iter < NIters; Iter++) {
if (! SamplePerm) {
// don't sample over permutations
CalcApxGraphDLL(); CalcApxGraphLL(); // fast
MyLL = LogLike; MyGradV = GradV;
} else {
// sample over permutations (approximate calculations)
SampleGradient(WarmUp, NSamples, MyLL, MyGradV);
}
double SumDiam=0, SumSngVal1=0, SumSngVal2=0;
for (int trial = 0; trial < AvgKGraphs; trial++) {
// generate kronecker graph
PNGraph KronGraph = TKronMtx::GenFastKronecker(ProbMtx, KronIters, true, 0); // approx
//PNGraph KronGraph = TKronMtx::GenKronecker(ProbMtx, KronIters, true, 0); // true
SngValV.Clr(true); TSnap::GetSngVals(KronGraph, 2, SngValV); SngValV.Sort(false);
SumDiam += TSnap::GetAnfEffDiam(KronGraph, false, 10);
SumSngVal1 += SngValV[0]; SumSngVal2 += SngValV[1];
}
// how good is the current fit
AvgLLV.Add(TFltPr(Iter, MyLL));
EZeroV.Add(TFltPr(Iter, ProbMtx.GetMtxSum()));
DiamV.Add(TFltPr(Iter, SumDiam/double(AvgKGraphs)));
Lambda1V.Add(TFltPr(Iter, SumSngVal1/double(AvgKGraphs)));
Lambda2V.Add(TFltPr(Iter, SumSngVal2/double(AvgKGraphs)));
TrueLLV.Add(TFltPr(Iter, TrueLL));
TrueEZeroV.Add(TFltPr(Iter, TrueEZero));
TrueDiamV.Add(TFltPr(Iter, TrueEffDiam));
TrueLambda1V.Add(TFltPr(Iter, TrueLambda1));
TrueLambda2V.Add(TFltPr(Iter, TrueLambda2));
if (Iter % 10 == 0) {
const TStr Desc = TStr::Fmt("%s. Iter: %d, G(%d, %d) K(%d, %d)", Desc1.Empty()?OutFNm.CStr():Desc1.CStr(),
Iter, Graph->GetNodes(), Graph->GetEdges(), ProbMtx.GetNodes(KronIters), ProbMtx.GetEdges(KronIters));
PlotTrueAndEst("LL."+OutFNm, Desc, "Average LL", AvgLLV, TrueLLV);
PlotTrueAndEst("E0."+OutFNm, Desc, "E0 (expected number of edges)", EZeroV, TrueEZeroV);
PlotTrueAndEst("Diam."+OutFNm+"-Diam", Desc, "Effective diameter", DiamV, TrueDiamV);
PlotTrueAndEst("Lambda1."+OutFNm, Desc, "Lambda 1", Lambda1V, TrueLambda1V);
PlotTrueAndEst("Lambda2."+OutFNm, Desc, "Lambda 2", Lambda2V, TrueLambda2V);
if (! TrueParam.Empty()) {
PlotTrueAndEst("AbsErr."+OutFNm, Desc, "Average Absolute Error", AvgAbsErrV, TFltPrV()); }
}
if (! TrueParam.Empty()) {
AvgAbsErr = TKronMtx::GetAvgAbsErr(ProbMtx, TrueParam);
AvgAbsErrV.Add(TFltPr(Iter, AvgAbsErr));
} else { AvgAbsErr = 1.0; }
// update parameters
AbsSumErr = fabs(ProbMtx.GetMtxSum() - TrueEZero);
// update parameters
for (int p = 0; p < GetParams(); p++) {
LearnRateV[p] *= 0.99;
while (fabs(LearnRateV[p]*MyGradV[p]) > 0.1) { LearnRateV[p] *= 0.99; printf(".");}
while (fabs(LearnRateV[p]*MyGradV[p]) < 0.002) { LearnRateV[p] *= (1.0/0.95); printf("*");}
printf(" %d] %f <-- %f + %9f Grad: %9.1f, Rate:%g\n", p, ProbMtx.At(p) + LearnRateV[p]*MyGradV[p],
ProbMtx.At(p), (double)(LearnRateV[p]*MyGradV[p]), MyGradV[p](), LearnRateV[p]());
ProbMtx.At(p) = ProbMtx.At(p) + LearnRateV[p]*MyGradV[p];
// box constraints
if (ProbMtx.At(p) > 1.0) { ProbMtx.At(p)=1.0; }
if (ProbMtx.At(p) < 0.001) { ProbMtx.At(p)=0.001; }
}
printf("%d] LL: %g, ", Iter, MyLL);
printf(" avgAbsErr: %.4f, absSumErr: %.4f, newLL: %.2f, deltaLL: %.2f\n", AvgAbsErr, AbsSumErr, MyLL, OldLL-MyLL);
if (AvgAbsErr < 0.001) { printf("***CONVERGED!\n"); break; }
printf("\n"); fflush(stdout);
ProbMtx.GetLLMtx(LLMtx); OldLL = MyLL;
}
TrueParam.Dump("True Thetas", true);
ProbMtx.Dump("Final Thetas", true);
printf(" AvgAbsErr: %f\n AbsSumErr: %f\n Iterations: %d\n", AvgAbsErr, AbsSumErr, Iter);
printf("Iteration run time: %s, sec: %g\n\n", IterTm.GetTmStr(), IterTm.GetSecs());
}
| void TKroneckerLL::InitLL | ( | const TFltV & | ParamV | ) |
Definition at line 996 of file kronecker.cpp.
Referenced by GradDescentConvergence(), TestSamplePerm(), and TKroneckerLL().
| void TKroneckerLL::InitLL | ( | const TKronMtx & | ParamMtx | ) |
Definition at line 1000 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Gen(), TKronMtx::GetLLMtx(), GradV, IAssert, TKronMtx::IsProbMtx(), TVec< TVal, TSizeTy >::Len(), LLMtx, LogLike, TKronMtx::NInf, ProbMtx, and TVec< TVal, TSizeTy >::PutAll().
{
IAssert(ParamMtx.IsProbMtx());
ProbMtx = ParamMtx;
ProbMtx.GetLLMtx(LLMtx);
LogLike = TKronMtx::NInf;
if (GradV.Len() != ProbMtx.Len()) {
GradV.Gen(ProbMtx.Len()); }
GradV.PutAll(0.0);
}
| void TKroneckerLL::InitLL | ( | const PNGraph & | GraphPt, |
| const TKronMtx & | ParamMtx | ||
| ) |
Definition at line 1010 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Gen(), TKronMtx::GetLLMtx(), GradV, IAssert, TKronMtx::IsProbMtx(), TVec< TVal, TSizeTy >::Len(), LLMtx, LogLike, TKronMtx::NInf, ProbMtx, TVec< TVal, TSizeTy >::PutAll(), and SetGraph().
{
IAssert(ParamMtx.IsProbMtx());
ProbMtx = ParamMtx;
ProbMtx.GetLLMtx(LLMtx);
SetGraph(GraphPt);
LogLike = TKronMtx::NInf;
if (GradV.Len() != ProbMtx.Len()) {
GradV.Gen(ProbMtx.Len()); }
GradV.PutAll(0.0);
}
| bool TKroneckerLL::IsLatentEdge | ( | const int & | NId1, |
| const int & | NId2 | ||
| ) | const [inline] |
Definition at line 175 of file kronecker.h.
References IsObsEdge().
{ return !IsObsEdge(NId1, NId2); }

| bool TKroneckerLL::IsLatentNode | ( | const int & | NId | ) | const [inline] |
Definition at line 174 of file kronecker.h.
References IsObsNode().
{ return !IsObsNode(NId); }

| bool TKroneckerLL::IsObsEdge | ( | const int & | NId1, |
| const int & | NId2 | ||
| ) | const [inline] |
Definition at line 173 of file kronecker.h.
References IAssert, and RealNodes.
Referenced by IsLatentEdge(), and SetRandomEdges().

| bool TKroneckerLL::IsObsNode | ( | const int & | NId | ) | const [inline] |
Definition at line 172 of file kronecker.h.
References IAssert, and RealNodes.
Referenced by IsLatentNode().

| void TKroneckerLL::MetroGibbsSampleNext | ( | const int & | WarmUp, |
| const bool | DLLUpdate = false |
||
| ) |
Definition at line 1503 of file kronecker.cpp.
References TNGraph::DelEdge(), TVec< TVal, TSizeTy >::DelLast(), GEdgeV, TKronMtx::GetApxNoEdgeDLL(), TKronMtx::GetApxNoEdgeLL(), TKronMtx::GetEdgeDLL(), TKronMtx::GetEdgeLL(), TRnd::GetUniDevInt(), GradV, Graph, IAssertR, KronIters, TVec< TVal, TSizeTy >::Last(), LEdgeV, TKronMtx::Len(), TVec< TVal, TSizeTy >::Len(), LLMtx, LogLike, LSelfEdge, SampleNextPerm(), SetRandomEdges(), UpdateGraphDLL(), TTriple< TVal1, TVal2, TVal3 >::Val1, TTriple< TVal1, TVal2, TVal3 >::Val2, and TTriple< TVal1, TVal2, TVal3 >::Val3.
Referenced by RunEStep(), and RunMStep().
{
int NId1 = 0, NId2 = 0, hit = 0, GId = 0;
TIntTr EdgeToRemove, NewEdge;
double RndAccept;
if(LEdgeV.Len()) {
for(int i = 0; i < WarmUp; i++) {
hit = TKronMtx::Rnd.GetUniDevInt(LEdgeV.Len());
NId1 = LEdgeV[hit].Val1; NId2 = LEdgeV[hit].Val2;
GId = LEdgeV[hit].Val3;
SetRandomEdges(1, true);
NewEdge = LEdgeV.Last();
RndAccept = (1.0 - exp(LLMtx.GetEdgeLL(NewEdge.Val1, NewEdge.Val2, KronIters))) / (1.0 - exp(LLMtx.GetEdgeLL(NId1, NId2, KronIters)));
RndAccept = (RndAccept > 1.0) ? 1.0 : RndAccept;
if(TKronMtx::Rnd.GetUniDev() > RndAccept) { // reject
Graph->DelEdge(NewEdge.Val1, NewEdge.Val2);
if(NewEdge.Val1 != NewEdge.Val2) { GEdgeV.DelLast(); }
else { LSelfEdge--; }
LEdgeV.DelLast();
} else { // accept
Graph->DelEdge(NId1, NId2);
LEdgeV[hit] = LEdgeV.Last();
LEdgeV.DelLast();
if(NId1 == NId2) {
LSelfEdge--;
if(NewEdge.Val1 != NewEdge.Val2) {
GEdgeV[GEdgeV.Len()-1].Val3 = hit;
}
} else {
IAssertR(GEdgeV.Last().Val3 >= 0, "Invalid indexing");
GEdgeV[GId] = GEdgeV.Last();
if(NewEdge.Val1 != NewEdge.Val2) {
GEdgeV[GId].Val3 = hit;
}
LEdgeV[GEdgeV[GId].Val3].Val3 = GId;
GEdgeV.DelLast();
}
LogLike += LLMtx.GetApxNoEdgeLL(EdgeToRemove.Val1, EdgeToRemove.Val2, KronIters) - LLMtx.GetEdgeLL(EdgeToRemove.Val1, EdgeToRemove.Val2, KronIters);
LogLike += -LLMtx.GetApxNoEdgeLL(NewEdge.Val1, NewEdge.Val2, KronIters) + LLMtx.GetEdgeLL(NewEdge.Val1, NewEdge.Val2, KronIters);
if(DLLUpdate) {
for (int p = 0; p < LLMtx.Len(); p++) {
GradV[p] += LLMtx.GetApxNoEdgeDLL(p, EdgeToRemove.Val1, EdgeToRemove.Val2, KronIters) - LLMtx.GetEdgeDLL(p, EdgeToRemove.Val1, EdgeToRemove.Val2, KronIters);
GradV[p] += -LLMtx.GetApxNoEdgeDLL(p, NewEdge.Val1, NewEdge.Val2, KronIters) + LLMtx.GetEdgeDLL(p, NewEdge.Val1, NewEdge.Val2, KronIters);
}
}
}
}
}
// CalcApxGraphLL();
for (int s = 0; s < WarmUp; s++) {
if(SampleNextPerm(NId1, NId2)) {
if(DLLUpdate) UpdateGraphDLL(NId1, NId2);
}
}
}


| void TKroneckerLL::MetroGibbsSampleSetup | ( | const int & | WarmUp | ) |
Definition at line 1476 of file kronecker.cpp.
References CalcApxGraphLL(), EMType, TKronMtx::GetDim(), TKronMtx::GetMtxSum(), kronEdgeMiss, kronFutureLink, KronIters, MissEdges, Nodes, ProbMtx, RealNodes, RestoreGraph(), SampleNextPerm(), and SetRandomEdges().
Referenced by RunEStep().
{
double alpha = log(ProbMtx.GetMtxSum()) / log(double(ProbMtx.GetDim()));
int NId1 = 0, NId2 = 0;
int NMissing;
RestoreGraph(false);
if(EMType == kronEdgeMiss) {
CalcApxGraphLL();
for (int s = 0; s < WarmUp; s++) SampleNextPerm(NId1, NId2);
}
if(EMType == kronFutureLink) {
NMissing = (int) (pow(ProbMtx.GetMtxSum(), KronIters) - pow(double(RealNodes), alpha));
} else if(EMType == kronEdgeMiss) {
NMissing = MissEdges;
} else {
NMissing = (int) (pow(ProbMtx.GetMtxSum(), KronIters) * (1.0 - pow(double(RealNodes) / double(Nodes), 2)));
}
NMissing = (NMissing < 1) ? 1 : NMissing;
SetRandomEdges(NMissing, true);
CalcApxGraphLL();
for (int s = 0; s < WarmUp; s++) SampleNextPerm(NId1, NId2);
}

| static PKroneckerLL TKroneckerLL::New | ( | ) | [inline, static] |
Definition at line 154 of file kronecker.h.
References TKroneckerLL().
{ return new TKroneckerLL(); }

| PKroneckerLL TKroneckerLL::New | ( | const PNGraph & | GraphPt, |
| const TKronMtx & | ParamMtx, | ||
| const double & | PermPSwapNd = 0.1 |
||
| ) | [static] |
Definition at line 797 of file kronecker.cpp.
References TKroneckerLL().
{
return new TKroneckerLL(GraphPt, ParamMtx, PermPSwapNd);
}

| PKroneckerLL TKroneckerLL::New | ( | const PNGraph & | GraphPt, |
| const TKronMtx & | ParamMtx, | ||
| const TIntV & | NodeIdPermV, | ||
| const double & | PermPSwapNd = 0.2 |
||
| ) | [static] |
Definition at line 801 of file kronecker.cpp.
References TKroneckerLL().
{
return new TKroneckerLL(GraphPt, ParamMtx, NodeIdPermV, PermPSwapNd);
}

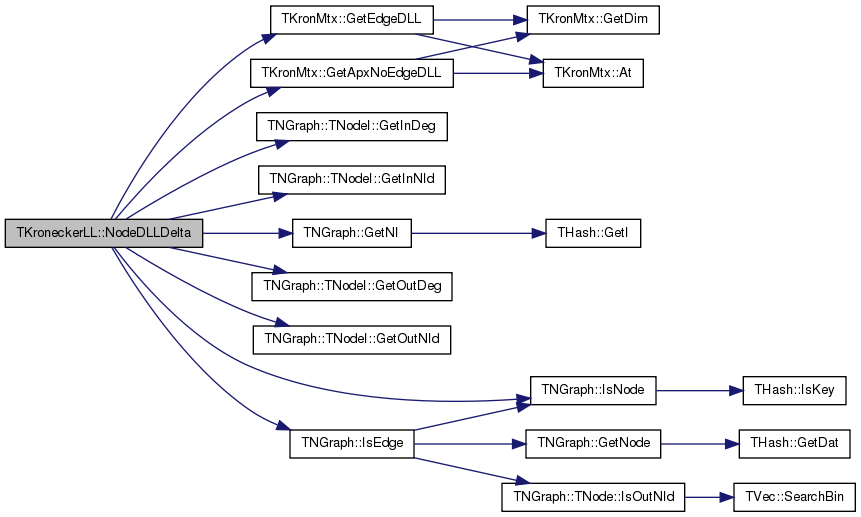
| double TKroneckerLL::NodeDLLDelta | ( | const int | ParamId, |
| const int & | NId | ||
| ) | const |
Definition at line 1214 of file kronecker.cpp.
References TKronMtx::GetApxNoEdgeDLL(), TKronMtx::GetEdgeDLL(), TNGraph::TNodeI::GetInDeg(), TNGraph::TNodeI::GetInNId(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), Graph, IAssert, TNGraph::IsEdge(), TNGraph::IsNode(), KronIters, LLMtx, and NodePerm.
Referenced by UpdateGraphDLL().
{
if (! Graph->IsNode(NId)) { return 0.0; } // zero degree node
double Delta = 0.0;
const TNGraph::TNodeI Node = Graph->GetNI(NId);
const int SrcRow = NodePerm[NId];
for (int e = 0; e < Node.GetOutDeg(); e++) {
const int DstCol = NodePerm[Node.GetOutNId(e)];
Delta += - LLMtx.GetApxNoEdgeDLL(ParamId, SrcRow, DstCol, KronIters)
+ LLMtx.GetEdgeDLL(ParamId, SrcRow, DstCol, KronIters);
}
const int SrcCol = NodePerm[NId];
for (int e = 0; e < Node.GetInDeg(); e++) {
const int DstRow = NodePerm[Node.GetInNId(e)];
Delta += - LLMtx.GetApxNoEdgeDLL(ParamId, DstRow, SrcCol, KronIters)
+ LLMtx.GetEdgeDLL(ParamId, DstRow, SrcCol, KronIters);
}
// double counter self-edge
if (Graph->IsEdge(NId, NId)) {
Delta += + LLMtx.GetApxNoEdgeDLL(ParamId, SrcRow, SrcCol, KronIters)
- LLMtx.GetEdgeDLL(ParamId, SrcRow, SrcCol, KronIters);
IAssert(SrcRow == SrcCol);
}
return Delta;
}
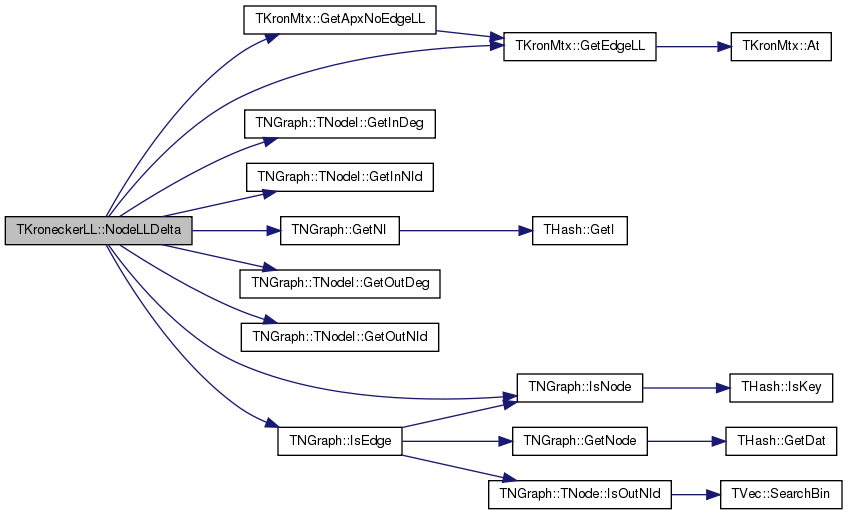
| double TKroneckerLL::NodeLLDelta | ( | const int & | NId | ) | const |
Definition at line 1055 of file kronecker.cpp.
References TKronMtx::GetApxNoEdgeLL(), TKronMtx::GetEdgeLL(), TNGraph::TNodeI::GetInDeg(), TNGraph::TNodeI::GetInNId(), TNGraph::GetNI(), TNGraph::TNodeI::GetOutDeg(), TNGraph::TNodeI::GetOutNId(), Graph, IAssert, TNGraph::IsEdge(), TNGraph::IsNode(), KronIters, LLMtx, and NodePerm.
Referenced by SwapNodesLL().
{
if (! Graph->IsNode(NId)) { return 0.0; } // zero degree node
double Delta = 0.0;
const TNGraph::TNodeI Node = Graph->GetNI(NId);
// out-edges
const int SrcRow = NodePerm[NId];
for (int e = 0; e < Node.GetOutDeg(); e++) {
const int DstCol = NodePerm[Node.GetOutNId(e)];
Delta += - LLMtx.GetApxNoEdgeLL(SrcRow, DstCol, KronIters)
+ LLMtx.GetEdgeLL(SrcRow, DstCol, KronIters);
}
//in-edges
const int SrcCol = NodePerm[NId];
for (int e = 0; e < Node.GetInDeg(); e++) {
const int DstRow = NodePerm[Node.GetInNId(e)];
Delta += - LLMtx.GetApxNoEdgeLL(DstRow, SrcCol, KronIters)
+ LLMtx.GetEdgeLL(DstRow, SrcCol, KronIters);
}
// double counted self-edge
if (Graph->IsEdge(NId, NId)) {
Delta += + LLMtx.GetApxNoEdgeLL(SrcRow, SrcCol, KronIters)
- LLMtx.GetEdgeLL(SrcRow, SrcCol, KronIters);
IAssert(SrcRow == SrcCol);
}
return Delta;
}
| void TKroneckerLL::RestoreGraph | ( | const bool | RestoreNodes = true | ) |
!!!!! MYUNGHWAN, CHECK!
Definition at line 923 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Clr(), TVec< TVal, TSizeTy >::Del(), TNGraph::DelEdge(), TNGraph::DelNode(), GEdgeV, TNGraph::GetNodes(), Graph, LEdgeV, TVec< TVal, TSizeTy >::Len(), LSelfEdge, and RealNodes.
Referenced by MetroGibbsSampleSetup(), and RunKronEM().
{
// remove from Graph
int NId1, NId2;
for (int e = 0; e < LEdgeV.Len(); e++) {
NId1 = LEdgeV[e].Val1; NId2 = LEdgeV[e].Val2;
Graph->DelEdge(NId1, NId2);
// GEdgeV.DelIfIn(LEdgeV[e]);
}
if(LEdgeV.Len() - LSelfEdge)
GEdgeV.Del(GEdgeV.Len() - LEdgeV.Len() + LSelfEdge, GEdgeV.Len() - 1);
LEdgeV.Clr();
LSelfEdge = 0;
if(RestoreNodes) {
for(int i = Graph->GetNodes()-1; i >= RealNodes; i--) {
Graph->DelNode(i);
}
}
}
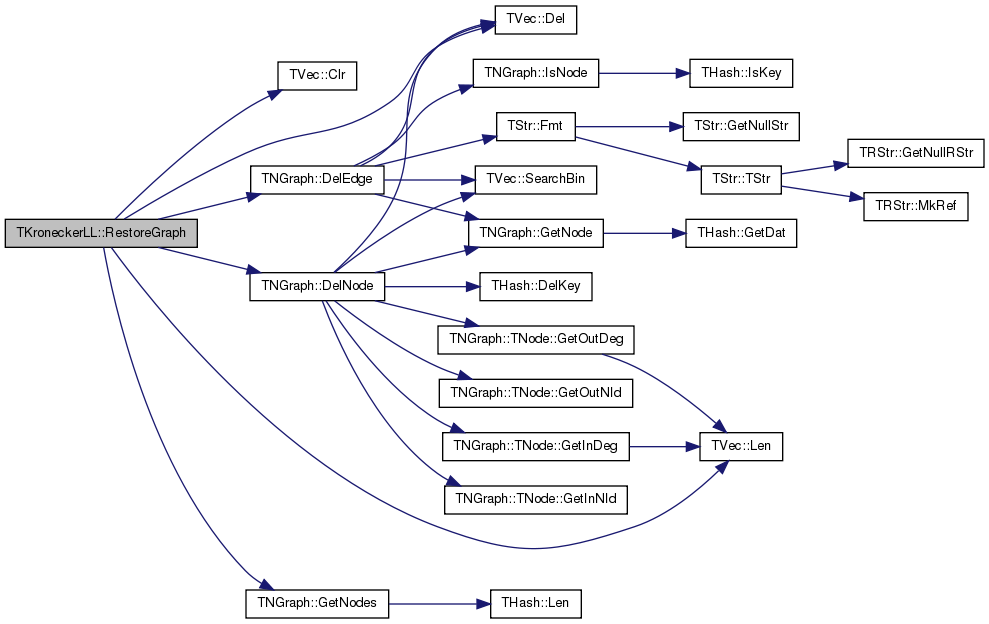

| void TKroneckerLL::RunEStep | ( | const int & | GibbsWarmUp, |
| const int & | WarmUp, | ||
| const int & | NSamples, | ||
| TFltV & | LLV, | ||
| TVec< TFltV > & | DLLV | ||
| ) |
Definition at line 1567 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), CalcApxGraphDLL(), CalcApxGraphLL(), TVec< TVal, TSizeTy >::Gen(), TExeTm::GetTmStr(), GradV, LogLike, MetroGibbsSampleNext(), MetroGibbsSampleSetup(), and TExeTm::Tick().
Referenced by RunKronEM().
{
TExeTm ExeTm, TotalTm;
LLV.Gen(NSamples, 0);
DLLV.Gen(NSamples, 0);
ExeTm.Tick();
for(int i = 0; i < 2; i++) MetroGibbsSampleSetup(WarmUp);
printf(" Warm-Up [%u] : %s\n", WarmUp, ExeTm.GetTmStr());
CalcApxGraphLL();
for(int i = 0; i < GibbsWarmUp; i++) MetroGibbsSampleNext(10, false);
printf(" Gibbs Warm-Up [%u] : %s\n", GibbsWarmUp, ExeTm.GetTmStr());
ExeTm.Tick();
CalcApxGraphLL();
CalcApxGraphDLL();
for(int i = 0; i < NSamples; i++) {
MetroGibbsSampleNext(50, false);
LLV.Add(LogLike);
DLLV.Add(GradV);
int OnePercent = (i+1) % (NSamples / 10);
if(OnePercent == 0) {
int TenPercent = ((i+1) / (NSamples / 10)) * 10;
printf(" %3u%% done : %s\n", TenPercent, ExeTm.GetTmStr());
}
}
}
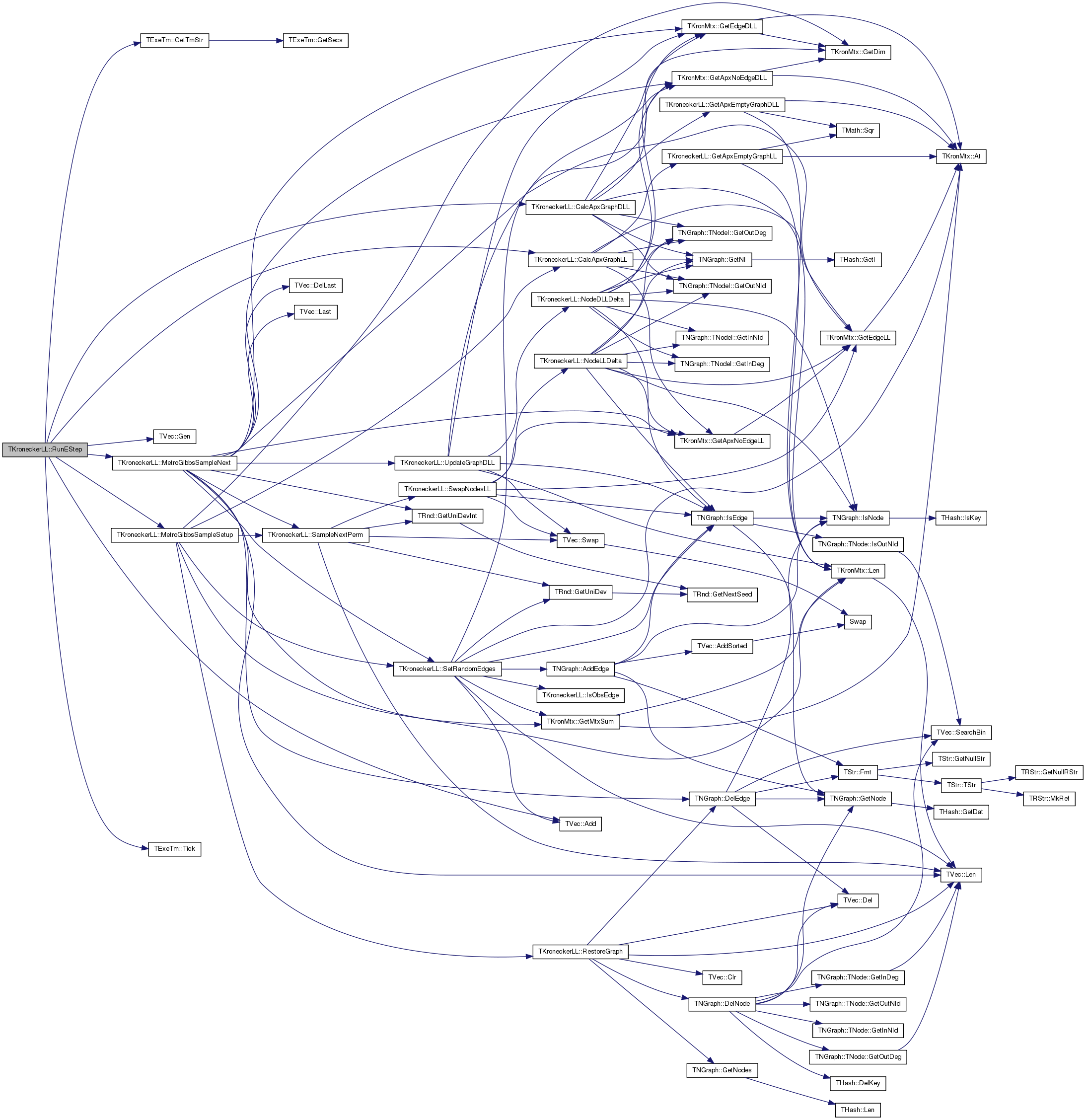

| void TKroneckerLL::RunKronEM | ( | const int & | EMIter, |
| const int & | GradIter, | ||
| double | LrnRate, | ||
| double | MnStep, | ||
| double | MxStep, | ||
| const int & | GibbsWarmUp, | ||
| const int & | WarmUp, | ||
| const int & | NSamples, | ||
| const TKronEMType & | Type = kronNodeMiss, |
||
| const int & | NMissing = -1 |
||
| ) |
Definition at line 1692 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), AppendIsoNodes(), DebugMode, EMType, TVec< TVal, TSizeTy >::Gen(), TKronMtx::GetNodes(), KronIters, LLV, MissEdges, MtxV, ProbMtx, RealEdges, RealNodes, RestoreGraph(), RunEStep(), RunMStep(), and SetRndPerm().
{
printf("\n----------------------------------------------------------------------\n");
printf("Fitting graph on %d nodes, %d edges\n", int(RealNodes), int(RealEdges));
printf("Kron iters: %d (== %d nodes)\n\n", KronIters(), ProbMtx.GetNodes(KronIters()));
TFltV LLV(NSamples);
TVec<TFltV> DLLV(NSamples);
//int count = 0;
EMType = Type;
MissEdges = NMissing;
AppendIsoNodes();
SetRndPerm();
if(DebugMode) {
LLV.Gen(EMIter, 0);
MtxV.Gen(EMIter, 0);
}
for(int i = 0; i < EMIter; i++) {
printf("\n----------------------------------------------------------------------\n");
printf("%03d EM-iter] E-Step\n", i+1);
RunEStep(GibbsWarmUp, WarmUp, NSamples, LLV, DLLV);
printf("\n\n");
printf("%03d EM-iter] M-Step\n", i+1);
double CurLL = RunMStep(LLV, DLLV, GradIter, LrnRate, MnStep, MxStep);
printf("\n\n");
if(DebugMode) {
LLV.Add(CurLL);
MtxV.Add(ProbMtx);
}
}
RestoreGraph();
}

| double TKroneckerLL::RunMStep | ( | const TFltV & | LLV, |
| const TVec< TFltV > & | DLLV, | ||
| const int & | GradIter, | ||
| const double & | LrnRate, | ||
| double | MnStep, | ||
| double | MxStep | ||
| ) |
Definition at line 1597 of file kronecker.cpp.
References TKronMtx::At(), CalcApxGraphDLL(), CalcApxGraphLL(), TKronMtx::Dump(), TKronMtx::GetDim(), TNGraph::GetEdges(), TKronMtx::GetLLMtx(), TKronMtx::GetMtxSum(), TNGraph::GetNodes(), GetParams(), TExeTm::GetTmStr(), GradV, Graph, TVec< TVal, TSizeTy >::Len(), LLMtx, LogLike, MetroGibbsSampleNext(), ProbMtx, RealEdges, RealNodes, and TExeTm::Tick().
Referenced by RunKronEM().
{
TExeTm IterTm, TotalTm;
double OldLL=LogLike, CurLL=0;
const double alpha = log(double(RealEdges)) / log(double(RealNodes));
const double EZero = pow(double(ProbMtx.GetDim()), alpha);
TFltV CurGradV(GetParams()), LearnRateV(GetParams()), LastStep(GetParams());
LearnRateV.PutAll(LrnRate);
TKronMtx NewProbMtx = ProbMtx;
const int NSamples = LLV.Len();
const int ReCalcLen = NSamples / 10;
for (int s = 0; s < LLV.Len(); s++) {
CurLL += LLV[s];
for(int p = 0; p < GetParams(); p++) { CurGradV[p] += DLLV[s][p]; }
}
CurLL /= NSamples;
for(int p = 0; p < GetParams(); p++) { CurGradV[p] /= NSamples; }
double MaxLL = CurLL;
TKronMtx MaxProbMtx = ProbMtx;
TKronMtx OldProbMtx = ProbMtx;
for (int Iter = 0; Iter < GradIter; Iter++) {
printf(" %03d] ", Iter+1);
IterTm.Tick();
for (int p = 0; p < GetParams(); p++) {
if (Iter < 1) {
while (fabs(LearnRateV[p]*CurGradV[p]) > MxStep) { LearnRateV[p] *= 0.95; }
while (fabs(LearnRateV[p]*CurGradV[p]) < 5 * MnStep) { LearnRateV[p] *= (1.0/0.95); } // move more
} else {
// set learn rate so that move for each parameter is inside the [MnStep, MxStep]
while (fabs(LearnRateV[p]*CurGradV[p]) > MxStep) { LearnRateV[p] *= 0.95; printf(".");}
while (fabs(LearnRateV[p]*CurGradV[p]) < MnStep) { LearnRateV[p] *= (1.0/0.95); printf("*");}
if (MxStep > 3*MnStep) { MxStep *= 0.95; }
}
NewProbMtx.At(p) = ProbMtx.At(p) + LearnRateV[p]*CurGradV[p];
if (NewProbMtx.At(p) > 0.9999) { NewProbMtx.At(p)=0.9999; }
if (NewProbMtx.At(p) < 0.0001) { NewProbMtx.At(p)=0.0001; }
LearnRateV[p] *= 0.95;
}
printf(" trueE0: %.2f (%u from %u), estE0: %.2f (%u from %u), ERR: %f\n", EZero, RealEdges(), RealNodes(), ProbMtx.GetMtxSum(), Graph->GetEdges(), Graph->GetNodes(), fabs(EZero-ProbMtx.GetMtxSum()));
printf(" currLL: %.4f, deltaLL: %.4f\n", CurLL, CurLL-OldLL); // positive is good
for (int p = 0; p < GetParams(); p++) {
printf(" %d] %f <-- %f + %9f Grad: %9.1f Rate: %g\n", p, NewProbMtx.At(p),
ProbMtx.At(p), (double)(LearnRateV[p]*CurGradV[p]), CurGradV[p](), LearnRateV[p]());
}
OldLL=CurLL;
if(Iter == GradIter - 1) {
break;
}
CurLL = 0;
CurGradV.PutAll(0.0);
TFltV OneDLL;
CalcApxGraphLL();
CalcApxGraphDLL();
for(int s = 0; s < NSamples; s++) {
ProbMtx = OldProbMtx; ProbMtx.GetLLMtx(LLMtx);
MetroGibbsSampleNext(10, true);
ProbMtx = NewProbMtx; ProbMtx.GetLLMtx(LLMtx);
if(s % ReCalcLen == ReCalcLen/2) {
CurLL += CalcApxGraphLL();
OneDLL = CalcApxGraphDLL();
} else {
CurLL += LogLike;
OneDLL = GradV;
}
for(int p = 0; p < GetParams(); p++) {
CurGradV[p] += OneDLL[p];
}
}
CurLL /= NSamples;
if(MaxLL < CurLL) {
MaxLL = CurLL; MaxProbMtx = ProbMtx;
}
printf(" Time: %s\n", IterTm.GetTmStr());
printf("\n"); fflush(stdout);
}
ProbMtx = MaxProbMtx; ProbMtx.GetLLMtx(LLMtx);
printf(" FinalLL : %f, TotalExeTm: %s\n", MaxLL, TotalTm.GetTmStr());
ProbMtx.Dump(" FITTED PARAMS", false);
return MaxLL;
}
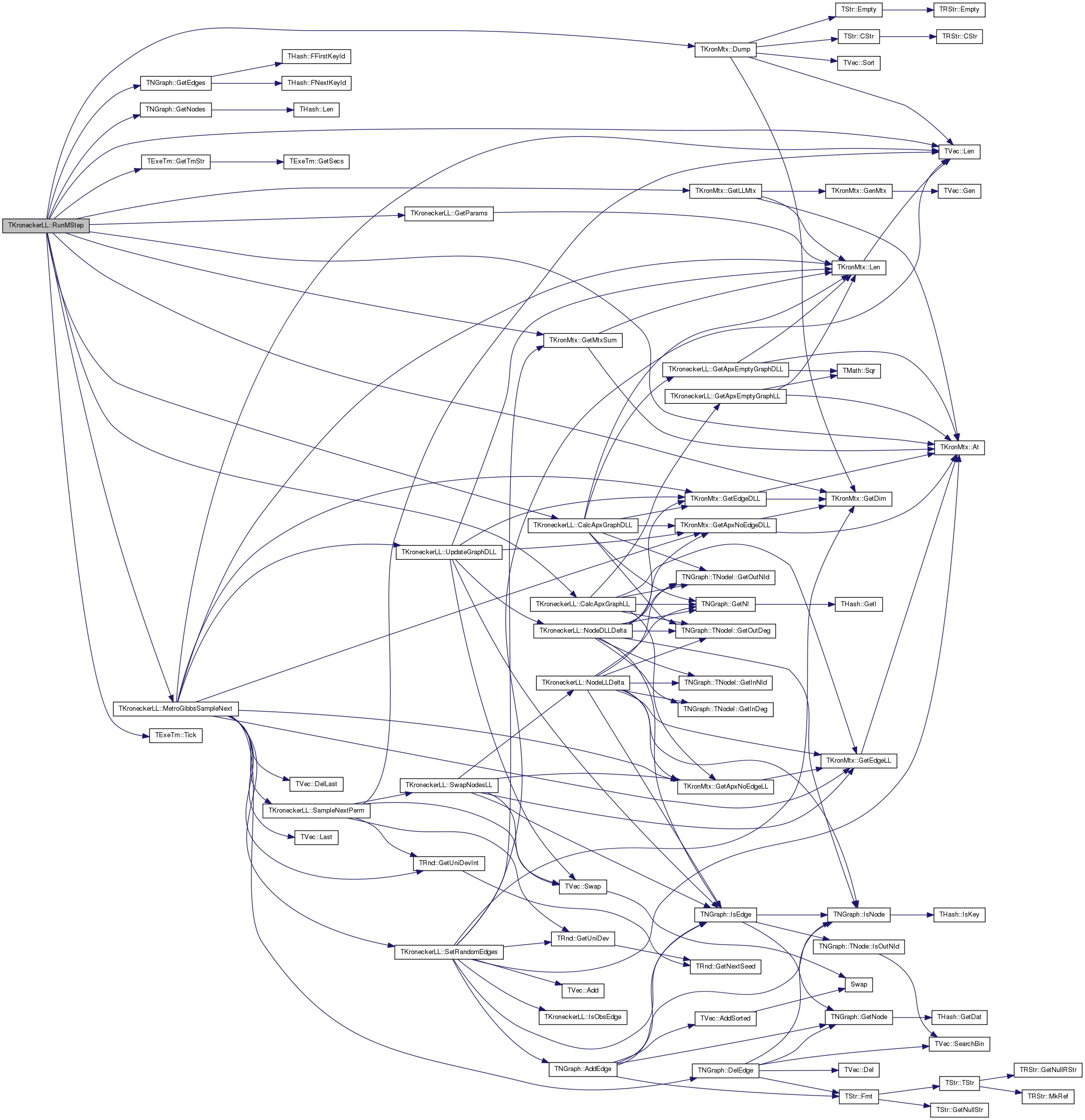

| void TKroneckerLL::SampleGradient | ( | const int & | WarmUp, |
| const int & | NSamples, | ||
| double & | AvgLL, | ||
| TFltV & | GradV | ||
| ) |
Definition at line 1271 of file kronecker.cpp.
References CalcApxGraphDLL(), CalcApxGraphLL(), TVec< TVal, TSizeTy >::Gen(), GetLL(), TInt::GetMegaStr(), TExeTm::GetSecs(), TExeTm::GetTmStr(), GradV, TKronMtx::Len(), LLMtx, TVec< TVal, TSizeTy >::PutAll(), SampleNextPerm(), TExeTm::Tick(), and UpdateGraphDLL().
Referenced by GradDescent(), GradDescent2(), GradDescentConvergence(), and TestKronDescent().
{
printf("SampleGradient: %s (%s warm-up):", TInt::GetMegaStr(NSamples).CStr(), TInt::GetMegaStr(WarmUp).CStr());
int NId1=0, NId2=0, NAccept=0;
TExeTm ExeTm1;
if (WarmUp > 0) {
CalcApxGraphLL();
for (int s = 0; s < WarmUp; s++) { SampleNextPerm(NId1, NId2); }
printf(" warm-up:%s,", ExeTm1.GetTmStr()); ExeTm1.Tick();
}
CalcApxGraphLL(); // re-calculate LL (due to numerical errors)
CalcApxGraphDLL();
AvgLL = 0;
AvgGradV.Gen(LLMtx.Len()); AvgGradV.PutAll(0.0);
printf(" sampl");
for (int s = 0; s < NSamples; s++) {
if (SampleNextPerm(NId1, NId2)) { // new permutation
UpdateGraphDLL(NId1, NId2); NAccept++; }
for (int m = 0; m < LLMtx.Len(); m++) { AvgGradV[m] += GradV[m]; }
AvgLL += GetLL();
}
printf("ing");
AvgLL = AvgLL / double(NSamples);
for (int m = 0; m < LLMtx.Len(); m++) {
AvgGradV[m] = AvgGradV[m] / double(NSamples); }
printf(":%s (%.0f/s), accept %.1f%%\n", ExeTm1.GetTmStr(), double(NSamples)/ExeTm1.GetSecs(),
double(100*NAccept)/double(NSamples));
}
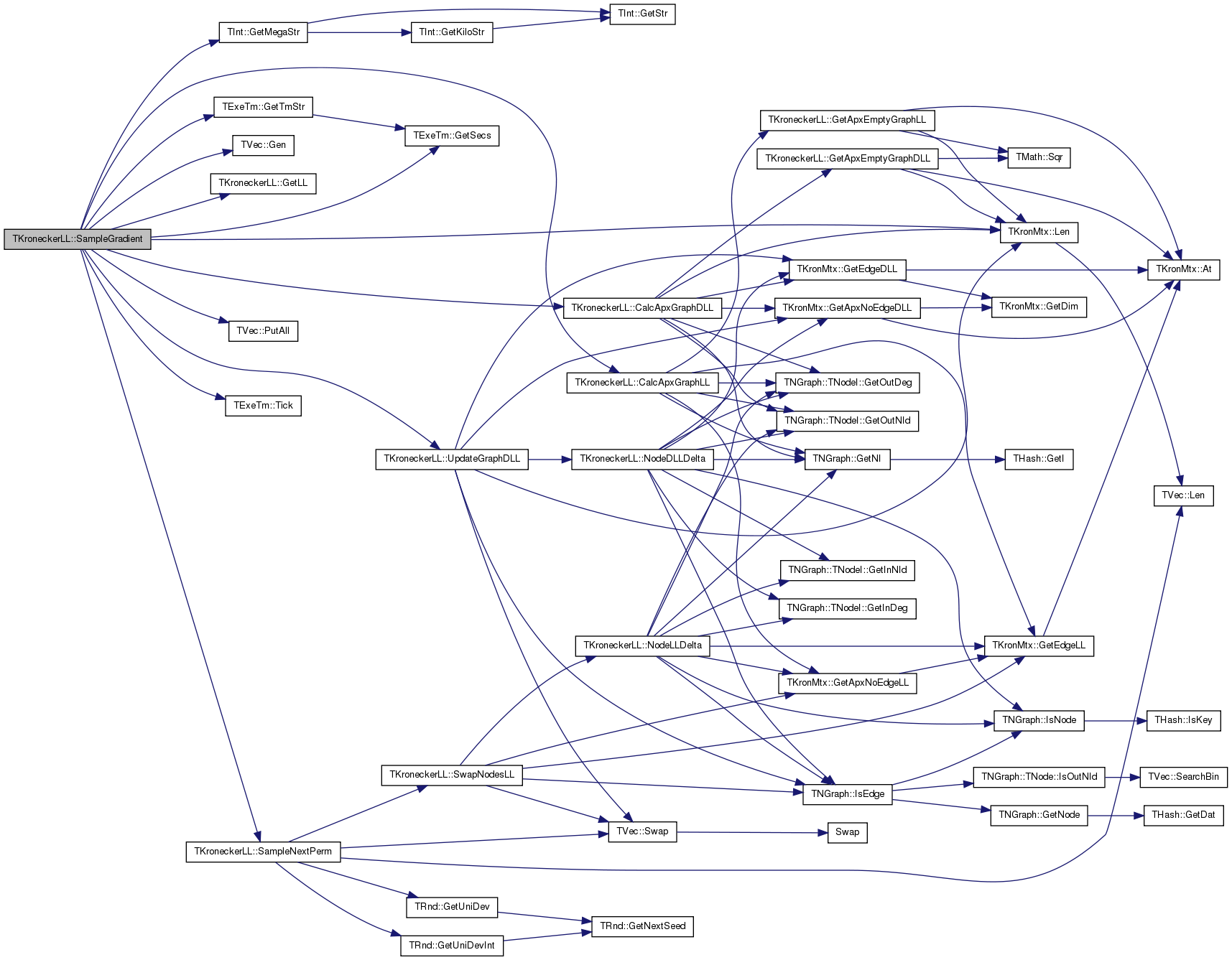

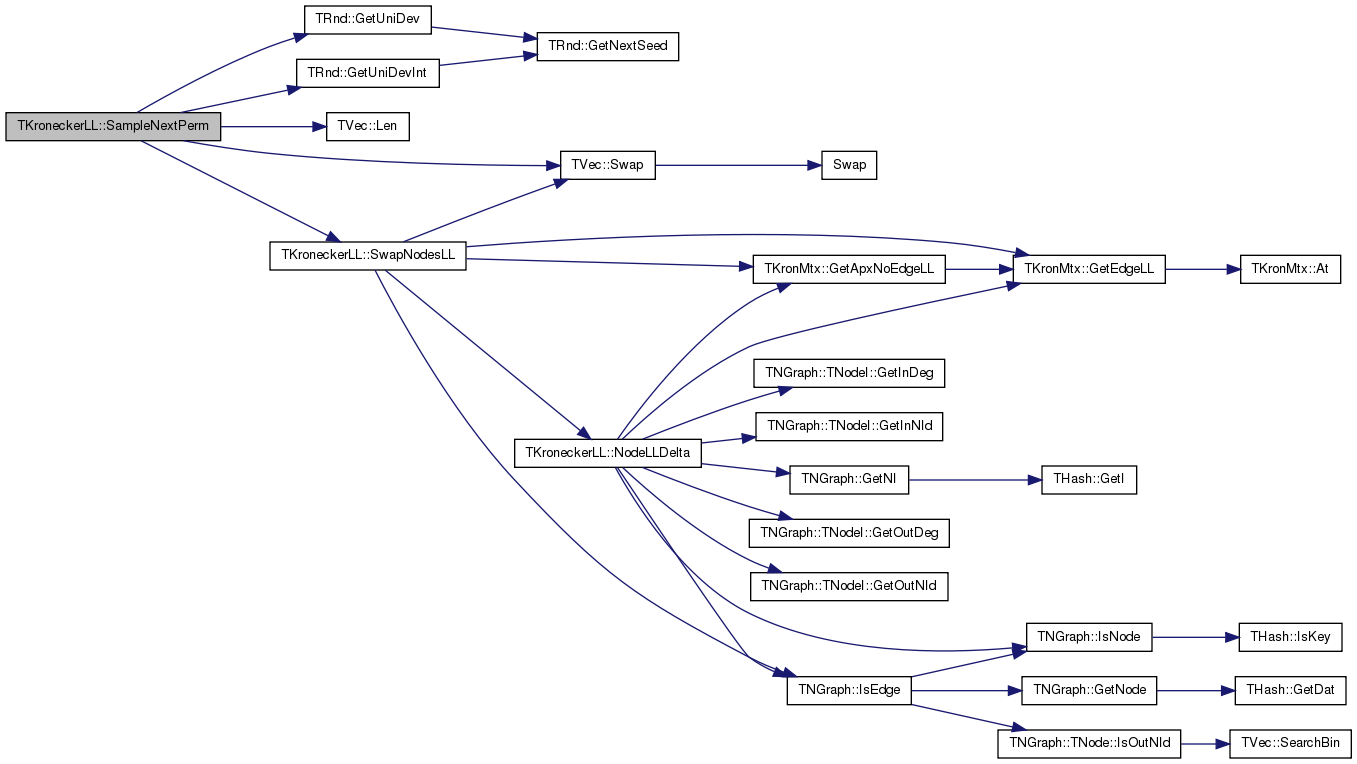
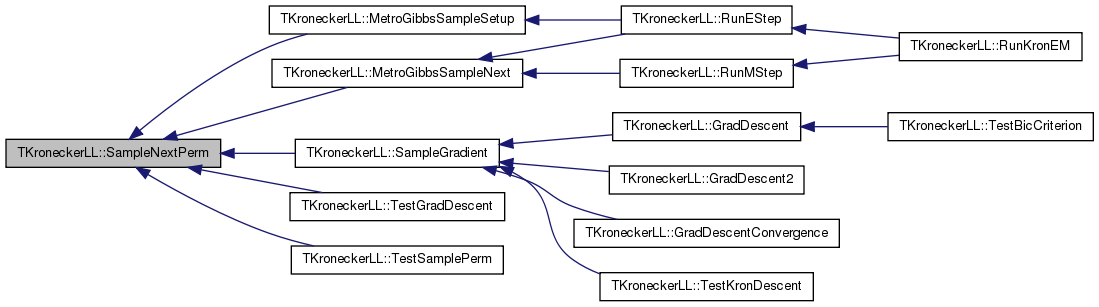
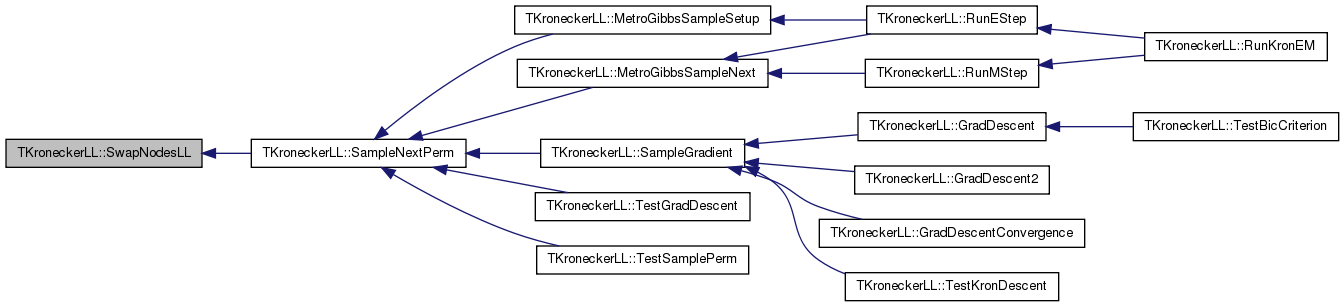
| bool TKroneckerLL::SampleNextPerm | ( | int & | NId1, |
| int & | NId2 | ||
| ) |
Definition at line 1111 of file kronecker.cpp.
References GEdgeV, TRnd::GetUniDev(), TRnd::GetUniDevInt(), InvertPerm, TVec< TVal, TSizeTy >::Len(), LogLike, NodePerm, Nodes, PermSwapNodeProb, TVec< TVal, TSizeTy >::Swap(), and SwapNodesLL().
Referenced by MetroGibbsSampleNext(), MetroGibbsSampleSetup(), SampleGradient(), TestGradDescent(), and TestSamplePerm().
{
// pick 2 uniform nodes and swap
if (TKronMtx::Rnd.GetUniDev() < PermSwapNodeProb) {
NId1 = TKronMtx::Rnd.GetUniDevInt(Nodes);
NId2 = TKronMtx::Rnd.GetUniDevInt(Nodes);
while (NId2 == NId1) { NId2 = TKronMtx::Rnd.GetUniDevInt(Nodes); }
} else {
// pick uniform edge and swap endpoints (slow as it moves around high degree nodes)
const int e = TKronMtx::Rnd.GetUniDevInt(GEdgeV.Len());
NId1 = GEdgeV[e].Val1; NId2 = GEdgeV[e].Val2;
}
const double U = TKronMtx::Rnd.GetUniDev();
const double OldLL = LogLike;
const double NewLL = SwapNodesLL(NId1, NId2);
const double LogU = log(U);
if (LogU > NewLL - OldLL) { // reject
LogLike = OldLL;
NodePerm.Swap(NId2, NId1); //swap back
InvertPerm.Swap(NodePerm[NId2], NodePerm[NId1]); // swap back
return false;
}
return true; // accept new sample
}
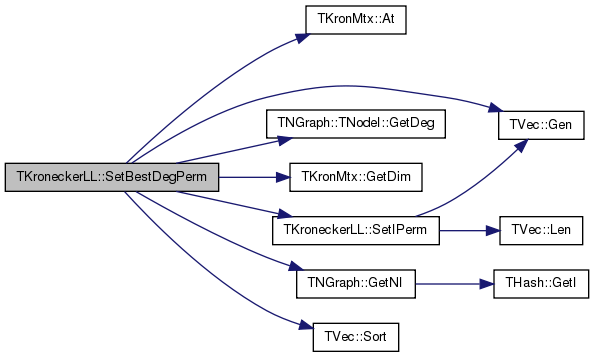
| void TKroneckerLL::SetBestDegPerm | ( | ) |
!!!!! MYUNGHWAN, CHECK!
Definition at line 842 of file kronecker.cpp.
References TKronMtx::At(), TVec< TVal, TSizeTy >::Gen(), TNGraph::TNodeI::GetDeg(), TKronMtx::GetDim(), TNGraph::GetNI(), Graph, KronIters, NodePerm, Nodes, ProbMtx, SetIPerm(), and TVec< TVal, TSizeTy >::Sort().
Referenced by SetPerm().
{
NodePerm.Gen(Nodes);
const int NZero = ProbMtx.GetDim();
TFltIntPrV DegV(Nodes), CDegV(Nodes);
TFltV Row(NZero);
TFltV Col(NZero);
for(int i = 0; i < NZero; i++) {
for(int j = 0; j < NZero; j++) {
Row[i] += ProbMtx.At(i, j);
Col[i] += ProbMtx.At(j, i);
}
}
for(int i = 0; i < Nodes; i++) {
TNGraph::TNodeI NodeI = Graph->GetNI(i);
int NId = i;
double RowP = 1.0, ColP = 1.0;
for(int j = 0; j < KronIters; j++) {
int Bit = NId % NZero;
RowP *= Row[Bit]; ColP *= Col[Bit];
NId /= NZero;
}
CDegV[i] = TFltIntPr(RowP + ColP, i);
DegV[i] = TFltIntPr(NodeI.GetDeg(), i);
}
DegV.Sort(false); CDegV.Sort(false);
for(int i = 0; i < Nodes; i++) {
NodePerm[DegV[i].Val2] = CDegV[i].Val2;
}
SetIPerm(NodePerm);
}

| void TKroneckerLL::SetDebug | ( | const bool | Debug | ) | [inline] |
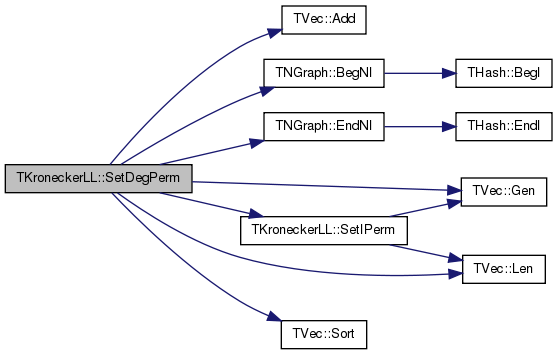
| void TKroneckerLL::SetDegPerm | ( | ) |
Definition at line 828 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TNGraph::BegNI(), TNGraph::EndNI(), TVec< TVal, TSizeTy >::Gen(), Graph, TVec< TVal, TSizeTy >::Len(), NodePerm, SetIPerm(), and TVec< TVal, TSizeTy >::Sort().
Referenced by GradDescentConvergence(), SetPerm(), TKronMaxLL::SetPerm(), TestGradDescent(), and TestKronDescent().
{
TIntPrV DegNIdV;
for (TNGraph::TNodeI NI = Graph->BegNI(); NI < Graph->EndNI(); NI++) {
DegNIdV.Add(TIntPr(NI.GetDeg(), NI.GetId()));
}
DegNIdV.Sort(false);
NodePerm.Gen(DegNIdV.Len(), 0);
for (int i = 0; i < DegNIdV.Len(); i++) {
NodePerm.Add(DegNIdV[i].Val2);
}
SetIPerm(NodePerm);
}
| void TKroneckerLL::SetGraph | ( | const PNGraph & | GraphPt | ) |
Definition at line 882 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TNGraph::BegEI(), TNGraph::EndEI(), GEdgeV, TVec< TVal, TSizeTy >::Gen(), TKronMtx::GetDim(), TNGraph::GetEdges(), TNGraph::GetNIdV(), TNGraph::GetNodes(), TSnap::GetSubGraph(), Graph, IAssert, TNGraph::IsNode(), KronIters, LEdgeV, TKronMtx::Len(), LLMtx, LSelfEdge, Nodes, ProbMtx, RealEdges, and RealNodes.
Referenced by InitLL().
{
Graph = GraphPt;
bool NodesOk = true;
// check that nodes IDs are {0,1,..,Nodes-1}
for (int nid = 0; nid < Graph->GetNodes(); nid++) {
if (! Graph->IsNode(nid)) { NodesOk=false; break; } }
if (! NodesOk) {
TIntV NIdV; GraphPt->GetNIdV(NIdV);
Graph = TSnap::GetSubGraph(GraphPt, NIdV, true);
for (int nid = 0; nid < Graph->GetNodes(); nid++) {
IAssert(Graph->IsNode(nid)); }
}
Nodes = Graph->GetNodes();
IAssert(LLMtx.GetDim() > 1 && LLMtx.Len() == ProbMtx.Len());
KronIters = (int) ceil(log(double(Nodes)) / log(double(ProbMtx.GetDim())));
// edge vector (for swap-edge permutation proposal)
// if (PermSwapNodeProb < 1.0) { /// !!!!! MYUNGHWAN, CHECK! WHY IS THIS COMMENTED OUT
GEdgeV.Gen(Graph->GetEdges(), 0);
for (TNGraph::TEdgeI EI = Graph->BegEI(); EI < Graph->EndEI(); EI++) {
if (EI.GetSrcNId() != EI.GetDstNId()) {
GEdgeV.Add(TIntTr(EI.GetSrcNId(), EI.GetDstNId(), -1));
}
}
// }
RealNodes = Nodes;
RealEdges = Graph->GetEdges();
LEdgeV = TIntTrV();
LSelfEdge = 0;
}

| void TKroneckerLL::SetIPerm | ( | const TIntV & | Perm | ) |
!!!!! MYUNGHWAN, CHECK!
Definition at line 875 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Gen(), InvertPerm, and TVec< TVal, TSizeTy >::Len().
Referenced by SetBestDegPerm(), SetDegPerm(), SetOrderPerm(), SetPerm(), SetRndPerm(), and TKroneckerLL().
{
InvertPerm.Gen(Perm.Len());
for (int i = 0; i < Perm.Len(); i++) {
InvertPerm[Perm[i]] = i;
}
}

| void TKroneckerLL::SetOrderPerm | ( | ) |
Definition at line 813 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Gen(), TNGraph::GetNodes(), Graph, NodePerm, Nodes, and SetIPerm().
Referenced by GradDescentConvergence(), SetPerm(), TKronMaxLL::SetPerm(), TestGradDescent(), TestKronDescent(), and TestSamplePerm().
{
NodePerm.Gen(Nodes, 0);
for (int i = 0; i < Graph->GetNodes(); i++) {
NodePerm.Add(i); }
SetIPerm(NodePerm);
}
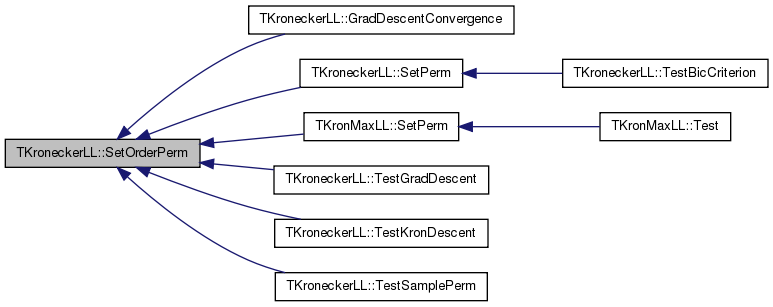
| void TKroneckerLL::SetPerm | ( | const char & | PermId | ) |
Definition at line 805 of file kronecker.cpp.
References FailR, SetBestDegPerm(), SetDegPerm(), SetOrderPerm(), and SetRndPerm().
Referenced by TestBicCriterion().
{
if (PermId == 'o') { SetOrderPerm(); }
else if (PermId == 'd') { SetDegPerm(); }
else if (PermId == 'r') { SetRndPerm(); }
else if (PermId == 'b') { SetBestDegPerm(); }
else FailR("Unknown permutation type (o,d,r)");
}
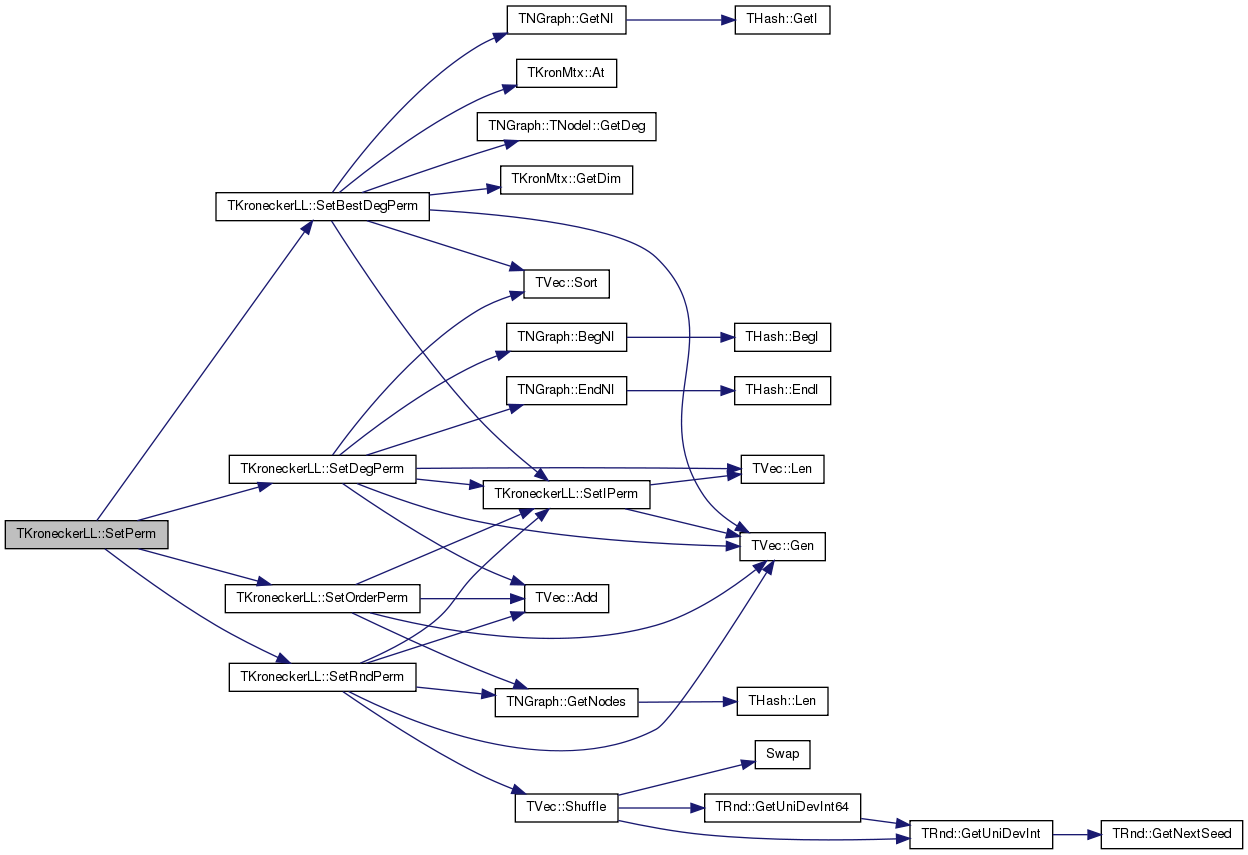

| void TKroneckerLL::SetPerm | ( | const TIntV & | NodePermV | ) | [inline] |
Definition at line 183 of file kronecker.h.
References NodePerm, and SetIPerm().
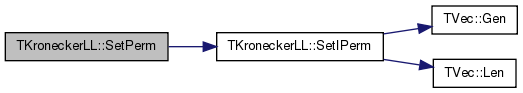
| void TKroneckerLL::SetRandomEdges | ( | const int & | NEdges, |
| const bool | isDir = true |
||
| ) |
!!!!! MYUNGHWAN, CHECK!
Definition at line 1417 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TNGraph::AddEdge(), TKronMtx::At(), EMType, GEdgeV, TKronMtx::GetDim(), TKronMtx::GetMtxSum(), TRnd::GetUniDev(), Graph, InvertPerm, TNGraph::IsEdge(), IsObsEdge(), kronEdgeMiss, KronIters, LEdgeV, TVec< TVal, TSizeTy >::Len(), LSelfEdge, Nodes, and ProbMtx.
Referenced by MetroGibbsSampleNext(), and MetroGibbsSampleSetup().
{
int count = 0, added = 0, collision = 0;
const int MtxDim = ProbMtx.GetDim();
const double MtxSum = ProbMtx.GetMtxSum();
TVec<TFltIntIntTr> ProbToRCPosV; // row, col position
double CumProb = 0.0;
for(int r = 0; r < MtxDim; r++) {
for(int c = 0; c < MtxDim; c++) {
const double Prob = ProbMtx.At(r, c);
if (Prob > 0.0) {
CumProb += Prob;
ProbToRCPosV.Add(TFltIntIntTr(CumProb/MtxSum, r, c));
}
}
}
int Rng, Row, Col, n, NId1, NId2;
while(added < NEdges) {
Rng = Nodes; Row = 0; Col = 0;
for (int iter = 0; iter < KronIters; iter++) {
const double& Prob = TKronMtx::Rnd.GetUniDev();
n = 0; while(Prob > ProbToRCPosV[n].Val1) { n++; }
const int MtxRow = ProbToRCPosV[n].Val2;
const int MtxCol = ProbToRCPosV[n].Val3;
Rng /= MtxDim;
Row += MtxRow * Rng;
Col += MtxCol * Rng;
}
count++;
NId1 = InvertPerm[Row]; NId2 = InvertPerm[Col];
// Check conflicts
if(EMType != kronEdgeMiss && IsObsEdge(NId1, NId2)) {
continue;
}
if (! Graph->IsEdge(NId1, NId2)) {
Graph->AddEdge(NId1, NId2);
if(NId1 != NId2) { GEdgeV.Add(TIntTr(NId1, NId2, LEdgeV.Len())); }
else { LSelfEdge++; }
LEdgeV.Add(TIntTr(NId1, NId2, GEdgeV.Len()-1));
added++;
if (! isDir) {
if (NId1 != NId2) {
Graph->AddEdge(NId2, NId1);
GEdgeV.Add(TIntTr(NId2, NId1, LEdgeV.Len()));
LEdgeV.Add(TIntTr(NId2, NId1, GEdgeV.Len()-1));
added++;
}
}
} else { collision ++; }
}
// printf("total = %d / added = %d / collision = %d\n", count, added, collision);
}
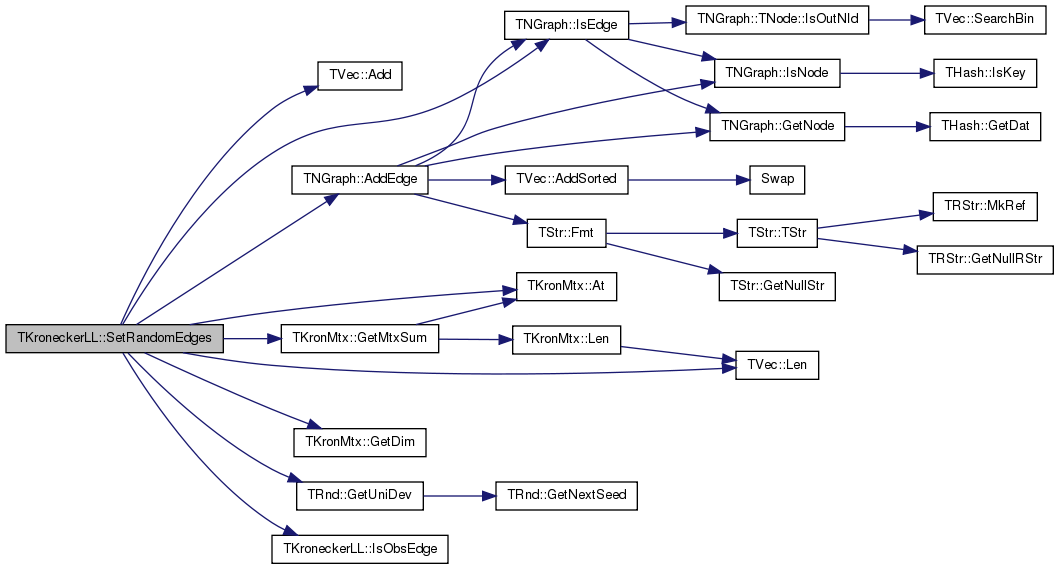

| void TKroneckerLL::SetRndPerm | ( | ) |
Definition at line 820 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TVec< TVal, TSizeTy >::Gen(), TNGraph::GetNodes(), Graph, NodePerm, Nodes, SetIPerm(), and TVec< TVal, TSizeTy >::Shuffle().
Referenced by RunKronEM(), SetPerm(), TKronMaxLL::SetPerm(), and TestGradDescent().
{
NodePerm.Gen(Nodes, 0);
for (int i = 0; i < Graph->GetNodes(); i++) {
NodePerm.Add(i); }
NodePerm.Shuffle(TKronMtx::Rnd);
SetIPerm(NodePerm);
}
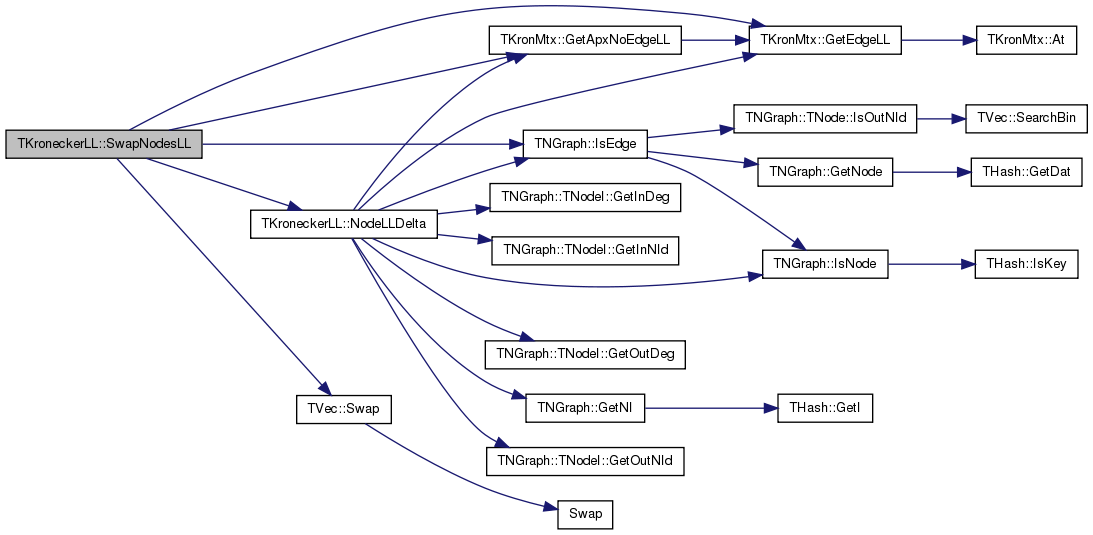
| double TKroneckerLL::SwapNodesLL | ( | const int & | NId1, |
| const int & | NId2 | ||
| ) |
Definition at line 1083 of file kronecker.cpp.
References TKronMtx::GetApxNoEdgeLL(), TKronMtx::GetEdgeLL(), Graph, InvertPerm, TNGraph::IsEdge(), KronIters, LLMtx, LogLike, NodeLLDelta(), NodePerm, and TVec< TVal, TSizeTy >::Swap().
Referenced by SampleNextPerm().
{
// subtract old LL (remove nodes)
LogLike = LogLike - NodeLLDelta(NId1) - NodeLLDelta(NId2);
const int PrevId1 = NodePerm[NId1], PrevId2 = NodePerm[NId2];
// double-counted edges
if (Graph->IsEdge(NId1, NId2)) {
LogLike += - LLMtx.GetApxNoEdgeLL(PrevId1, PrevId2, KronIters)
+ LLMtx.GetEdgeLL(PrevId1, PrevId2, KronIters); }
if (Graph->IsEdge(NId2, NId1)) {
LogLike += - LLMtx.GetApxNoEdgeLL(PrevId2, PrevId1, KronIters)
+ LLMtx.GetEdgeLL(PrevId2, PrevId1, KronIters); }
// swap
NodePerm.Swap(NId1, NId2);
InvertPerm.Swap(NodePerm[NId1], NodePerm[NId2]);
// add new LL (add nodes)
LogLike = LogLike + NodeLLDelta(NId1) + NodeLLDelta(NId2);
const int NewId1 = NodePerm[NId1], NewId2 = NodePerm[NId2];
// correct for double-counted edges
if (Graph->IsEdge(NId1, NId2)) {
LogLike += + LLMtx.GetApxNoEdgeLL(NewId1, NewId2, KronIters)
- LLMtx.GetEdgeLL(NewId1, NewId2, KronIters); }
if (Graph->IsEdge(NId2, NId1)) {
LogLike += + LLMtx.GetApxNoEdgeLL(NewId2, NewId1, KronIters)
- LLMtx.GetEdgeLL(NewId2, NewId1, KronIters); }
return LogLike;
}
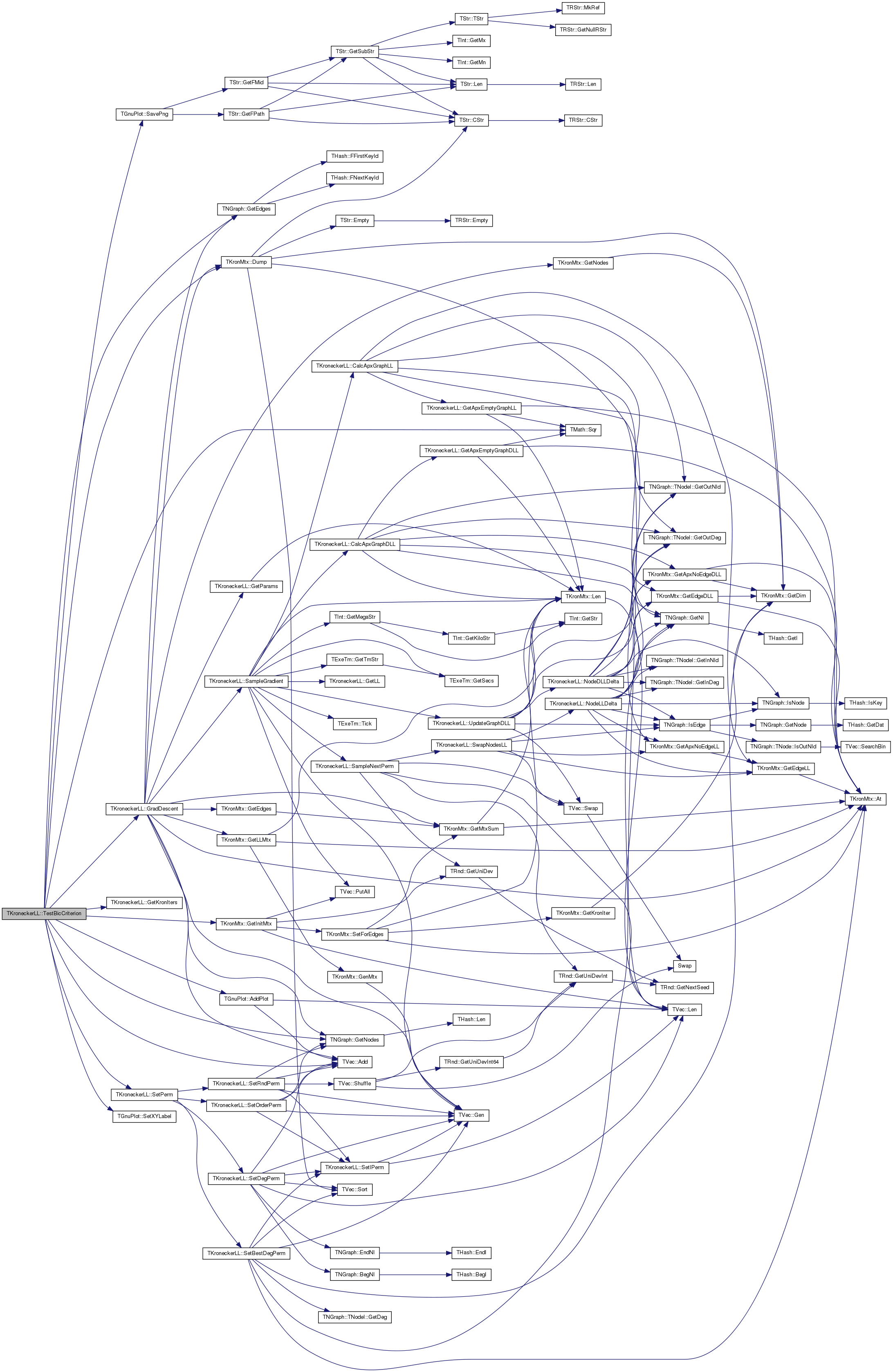
| void TKroneckerLL::TestBicCriterion | ( | const TStr & | OutFNm, |
| const TStr & | Desc1, | ||
| const PNGraph & | G, | ||
| const int & | GradIters, | ||
| double | LearnRate, | ||
| const int & | WarmUp, | ||
| const int & | NSamples, | ||
| const int & | TrueN0 | ||
| ) | [static] |
Definition at line 2109 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TGnuPlot::AddPlot(), TKronMtx::Dump(), TNGraph::GetEdges(), TKronMtx::GetInitMtx(), GetKronIters(), TNGraph::GetNodes(), gpwLinesPoints, GradDescent(), LLV, TGnuPlot::SavePng(), SetPerm(), TGnuPlot::SetXYLabel(), and TMath::Sqr().
{
TFltPrV BicV, MdlV, LLV;
const double rndGP = G->GetEdges()/TMath::Sqr(double(G->GetNodes()));
const double RndGLL = G->GetEdges()*log(rndGP )+ (TMath::Sqr(double(G->GetNodes()))-G->GetEdges())*log(1-rndGP);
LLV.Add(TFltPr(1, RndGLL));
BicV.Add(TFltPr(1, -RndGLL + 0.5*TMath::Sqr(1)*log(TMath::Sqr(G->GetNodes()))));
MdlV.Add(TFltPr(1, -RndGLL + 32*TMath::Sqr(1)+2*(log((double)1)+log((double)G->GetNodes()))));
for (int NZero = 2; NZero < 10; NZero++) {
const TKronMtx InitKronMtx = TKronMtx::GetInitMtx(NZero, G->GetNodes(), G->GetEdges());
InitKronMtx.Dump("INIT PARAM", true);
TKroneckerLL KronLL(G, InitKronMtx);
KronLL.SetPerm('d'); // degree perm
const double LastLL = KronLL.GradDescent(GradIters, LearnRate, 0.001, 0.01, WarmUp, NSamples);
LLV.Add(TFltPr(NZero, LastLL));
BicV.Add(TFltPr(NZero, -LastLL + 0.5*TMath::Sqr(NZero)*log(TMath::Sqr(G->GetNodes()))));
MdlV.Add(TFltPr(NZero, -LastLL + 32*TMath::Sqr(NZero)+2*(log((double)NZero)+log((double)KronLL.GetKronIters()))));
{ TGnuPlot GP("LL-"+OutFNm, Desc1);
GP.AddPlot(LLV, gpwLinesPoints, "Log-likelihood", "linewidth 1 pointtype 6 pointsize 2");
GP.SetXYLabel("NZero", "Log-Likelihood"); GP.SavePng(); }
{ TGnuPlot GP("BIC-"+OutFNm, Desc1);
GP.AddPlot(BicV, gpwLinesPoints, "BIC", "linewidth 1 pointtype 6 pointsize 2");
GP.SetXYLabel("NZero", "BIC"); GP.SavePng(); }
{ TGnuPlot GP("MDL-"+OutFNm, Desc1);
GP.AddPlot(MdlV, gpwLinesPoints, "MDL", "linewidth 1 pointtype 6 pointsize 2");
GP.SetXYLabel("NZero", "MDL"); GP.SavePng(); }
}
}
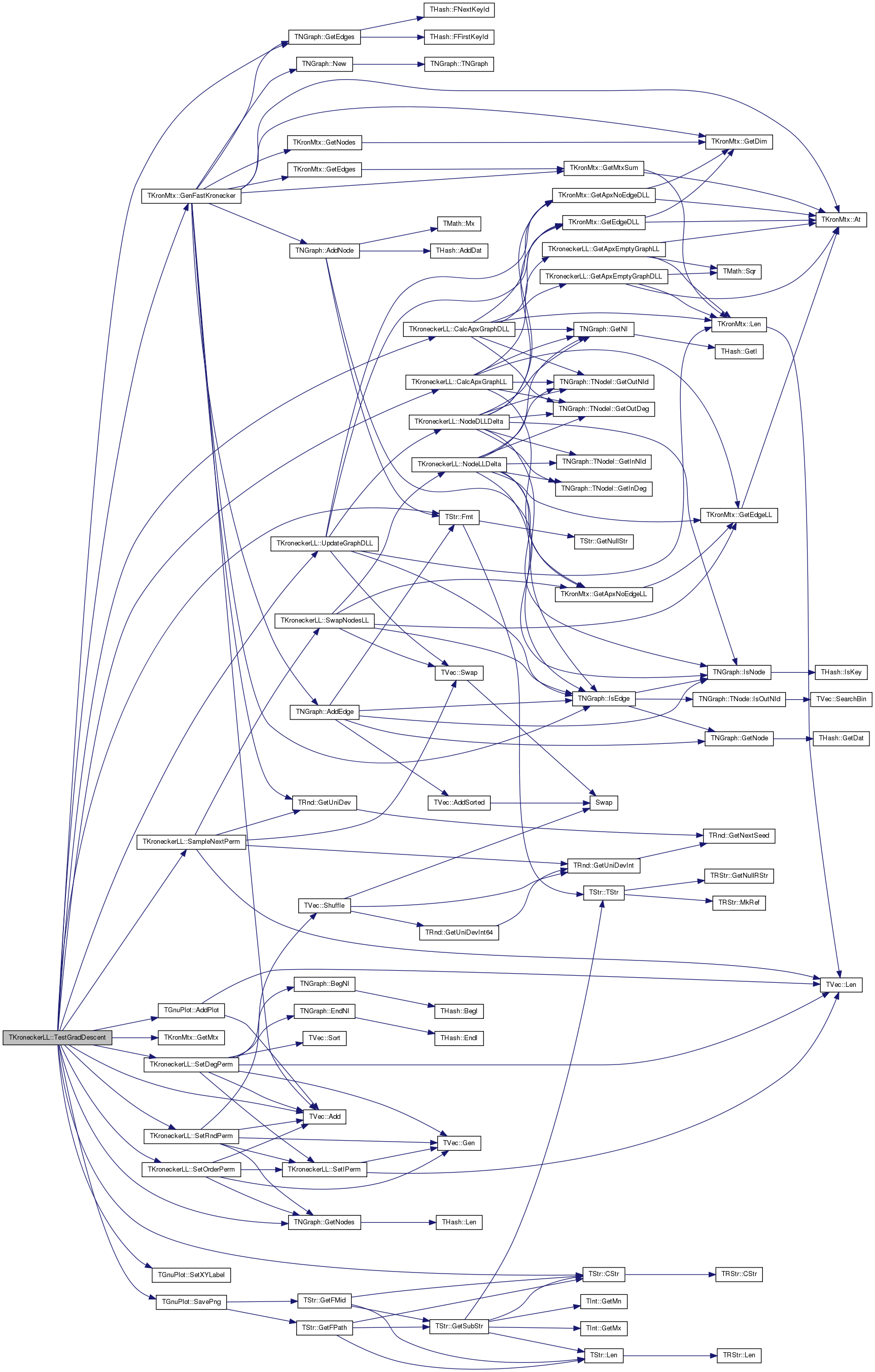
| void TKroneckerLL::TestGradDescent | ( | const int & | KronIters, |
| const int & | KiloSamples, | ||
| const TStr & | Permutation | ||
| ) | [static] |
Definition at line 2138 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), TGnuPlot::AddPlot(), CalcApxGraphDLL(), CalcApxGraphLL(), TStr::CStr(), FailR, TStr::Fmt(), TKronMtx::GenFastKronecker(), TNGraph::GetEdges(), TKronMtx::GetMtx(), TNGraph::GetNodes(), gpwLines, GradV, Graph, KronIters, SampleNextPerm(), TGnuPlot::SavePng(), SetDegPerm(), SetOrderPerm(), SetRndPerm(), TGnuPlot::SetXYLabel(), and UpdateGraphDLL().
{
const TStr OutFNm = TStr::Fmt("grad-%s%d-%dk", Permutation.CStr(), KronIters, KiloSamples);
TKronMtx KronParam = TKronMtx::GetMtx("0.8 0.6; 0.6 0.4");
PNGraph Graph = TKronMtx::GenFastKronecker(KronParam, KronIters, true, 0);
TKroneckerLL KronLL(Graph, KronParam);
TVec<TFltV> GradVV(4), SDevVV(4); TFltV XValV;
int NId1 = 0, NId2 = 0, NAccept = 0;
TVec<TMom> GradMomV(4);
TExeTm ExeTm;
if (Permutation == "r") KronLL.SetRndPerm();
else if (Permutation == "d") KronLL.SetDegPerm();
else if (Permutation == "o") KronLL.SetOrderPerm();
else FailR("Unknown permutation (r,d,o)");
KronLL.CalcApxGraphLL();
KronLL.CalcApxGraphDLL();
for (int s = 0; s < 1000*KiloSamples; s++) {
if (KronLL.SampleNextPerm(NId1, NId2)) { // new permutation
KronLL.UpdateGraphDLL(NId1, NId2); NAccept++; }
if (s > 50000) { //warm up period
for (int m = 0; m < 4; m++) { GradVV[m].Add(KronLL.GradV[m]); }
if ((s+1) % 1000 == 0) {
printf(".");
for (int m = 0; m < 4; m++) { GradVV[m].Add(KronLL.GradV[m]); }
XValV.Add((s+1));
if ((s+1) % 100000 == 0) {
TGnuPlot GP(OutFNm, TStr::Fmt("Gradient vs. samples. %d nodes, %d edges", Graph->GetNodes(), Graph->GetEdges()), true);
for (int g = 0; g < GradVV.Len(); g++) {
GP.AddPlot(XValV, GradVV[g], gpwLines, TStr::Fmt("grad %d", g)); }
GP.SetXYLabel("sample index","log Gradient");
GP.SavePng();
}
}
}
}
printf("\n");
for (int m = 0; m < 4; m++) {
GradMomV[m].Def();
printf("grad %d: mean: %12f sDev: %12f median: %12f\n", m,
GradMomV[m].GetMean(), GradMomV[m].GetSDev(), GradMomV[m].GetMedian());
}
}
| TFltQu TKroneckerLL::TestKronDescent | ( | const bool & | DoExact, |
| const bool & | TruePerm, | ||
| double | LearnRate, | ||
| const int & | WarmUp, | ||
| const int & | NSamples, | ||
| const TKronMtx & | TrueParam | ||
| ) |
Definition at line 1942 of file kronecker.cpp.
References TKronMtx::At(), CalcApxGraphDLL(), CalcApxGraphLL(), CalcGraphDLL(), CalcGraphLL(), TKronMtx::Dump(), TKronMtx::GetAvgAbsErr(), TKronMtx::GetLLMtx(), TKronMtx::GetMtxSum(), GetParams(), TExeTm::GetSecs(), TExeTm::GetTmStr(), GradV, LLMtx, LogLike, ProbMtx, TVec< TVal, TSizeTy >::PutAll(), SampleGradient(), SetDegPerm(), and SetOrderPerm().
{
printf("Test gradient descent on a synthetic kronecker graphs:\n");
if (DoExact) { printf(" -- Exact gradient calculations\n"); }
else { printf(" -- Approximate gradient calculations\n"); }
if (TruePerm) { printf(" -- No permutation sampling (use true permutation)\n"); }
else { printf(" -- Sample permutations (start with degree permutation)\n"); }
TExeTm IterTm;
int Iter;
double OldLL=0, MyLL=0, AvgAbsErr, AbsSumErr;
TFltV MyGradV, SDevV;
TFltV LearnRateV(GetParams()); LearnRateV.PutAll(LearnRate);
if (TruePerm) {
SetOrderPerm();
}
else {
/*printf("SET EIGEN VECTOR PERMUTATIONS\n");
TFltV LeftSV, RightSV;
TGSvd::GetSngVec(Graph, LeftSV, RightSV);
TFltIntPrV V;
for (int v=0; v<LeftSV.Len();v++) { V.Add(TFltIntPr(LeftSV[v], v)); }
V.Sort(false);
NodePerm.Gen(Nodes, 0);
for (int v=0; v < V.Len();v++) { NodePerm.Add(V[v].Val2); } //*/
//printf("RANDOM PERMUTATION\n"); SetRndPerm();
printf("DEGREE PERMUTATION\n"); SetDegPerm();
}
for (Iter = 0; Iter < 100; Iter++) {
if (TruePerm) {
// don't sample over permutations
if (DoExact) { CalcGraphDLL(); CalcGraphLL(); } // slow, O(N^2)
else { CalcApxGraphDLL(); CalcApxGraphLL(); } // fast
MyLL = LogLike; MyGradV = GradV;
} else {
printf(".");
// sample over permutations (approximate calculations)
SampleGradient(WarmUp, NSamples, MyLL, MyGradV);
}
printf("%d] LL: %g, ", Iter, MyLL);
AvgAbsErr = TKronMtx::GetAvgAbsErr(ProbMtx, TrueParam);
AbsSumErr = fabs(ProbMtx.GetMtxSum() - TrueParam.GetMtxSum());
printf(" avgAbsErr: %.4f, absSumErr: %.4f, newLL: %.2f, deltaLL: %.2f\n", AvgAbsErr, AbsSumErr, MyLL, OldLL-MyLL);
for (int p = 0; p < GetParams(); p++) {
// set learn rate so that move for each parameter is inside the [0.01, 0.1]
LearnRateV[p] *= 0.9;
//printf("%d: rate: %f delta:%f\n", p, LearnRateV[p], fabs(LearnRateV[p]*MyGradV[p]));
while (fabs(LearnRateV[p]*MyGradV[p]) > 0.1) { LearnRateV[p] *= 0.9; }
//printf(" rate: %f delta:%f\n", LearnRateV[p], fabs(LearnRateV[p]*MyGradV[p]));
while (fabs(LearnRateV[p]*MyGradV[p]) < 0.001) { LearnRateV[p] *= (1.0/0.9); }
//printf(" rate: %f delta:%f\n", LearnRateV[p], fabs(LearnRateV[p]*MyGradV[p]));
printf(" %d] %f <-- %f + %f lrnRate:%g\n", p, ProbMtx.At(p) + LearnRateV[p]*MyGradV[p],
ProbMtx.At(p), (double)(LearnRateV[p]*MyGradV[p]), LearnRateV[p]());
ProbMtx.At(p) = ProbMtx.At(p) + LearnRateV[p]*MyGradV[p];
// box constraints
if (ProbMtx.At(p) > 0.99) { ProbMtx.At(p)=0.99; }
if (ProbMtx.At(p) < 0.01) { ProbMtx.At(p)=0.01; }
}
ProbMtx.GetLLMtx(LLMtx); OldLL = MyLL;
if (AvgAbsErr < 0.01) { printf("***CONVERGED!\n"); break; }
printf("\n"); fflush(stdout);
}
TrueParam.Dump("True Thetas", true);
ProbMtx.Dump("Final Thetas", true);
printf(" AvgAbsErr: %f\n AbsSumErr: %f\n Iterations: %d\n", AvgAbsErr, AbsSumErr, Iter);
printf("Iteration run time: %s, sec: %g\n\n", IterTm.GetTmStr(), IterTm.GetSecs());
return TFltQu(AvgAbsErr, AbsSumErr, Iter, IterTm.GetSecs());
}

| TFltV TKroneckerLL::TestSamplePerm | ( | const TStr & | OutFNm, |
| const int & | WarmUp, | ||
| const int & | NSamples, | ||
| const TKronMtx & | TrueMtx, | ||
| const bool & | DoPlot = true |
||
| ) |
Definition at line 1795 of file kronecker.cpp.
References TVec< TVal, TSizeTy >::Add(), CalcApxGraphDLL(), CalcApxGraphLL(), TStr::CStr(), TKronMtx::Dump(), TKronMtx::Empty(), TStr::Fmt(), TVec< TVal, TSizeTy >::Gen(), TNGraph::GetEdges(), GetLL(), TInt::GetMegaStr(), TNGraph::GetNodes(), GetParams(), TExeTm::GetSecs(), TExeTm::GetTmStr(), GradV, Graph, InitLL(), TVec< TVal, TSizeTy >::Len(), LogLike, NodePerm, PermSwapNodeProb, PlotAutoCorrelation(), PlotGrad(), ProbMtx, TVec< TVal, TSizeTy >::PutAll(), SampleNextPerm(), SetOrderPerm(), TExeTm::Tick(), and UpdateGraphDLL().
{
printf("Sample permutations: %s (warm-up: %s)\n", TInt::GetMegaStr(NSamples).CStr(), TInt::GetMegaStr(WarmUp).CStr());
int NId1=0, NId2=0, NAccept=0;
TExeTm ExeTm;
const int PlotLen = NSamples/1000+1;
double TrueLL=-1, AvgLL=0.0;
TFltV AvgGradV(GetParams());
TFltPrV TrueLLV(PlotLen, 0); // true log-likelihood (under the correct permutation)
TFltPrV EstLLV(PlotLen, 0); // estiamted log-likelihood (averaged over last 1k permutation)
TFltPrV AcceptV; // sample acceptance ratio
TFltV SampleLLV(NSamples, 0);
TVec<TFltPrV> GradVV(GetParams());
for (int g = 0; g < GetParams(); g++) {
GradVV[g].Gen(PlotLen, 0); }
if (! TrueMtx.Empty()) {
TIntV PermV=NodePerm; TKronMtx CurMtx=ProbMtx; ProbMtx.Dump();
InitLL(TrueMtx); SetOrderPerm(); CalcApxGraphLL(); printf("TrueLL: %f\n", LogLike());
TrueLL=LogLike; InitLL(CurMtx); NodePerm=PermV;
}
CalcApxGraphLL();
printf("LogLike at start: %f\n", LogLike());
if (WarmUp > 0) {
EstLLV.Add(TFltPr(0, LogLike));
if (TrueLL != -1) { TrueLLV.Add(TFltPr(0, TrueLL)); }
for (int s = 0; s < WarmUp; s++) { SampleNextPerm(NId1, NId2); }
printf(" warm-up:%s,", ExeTm.GetTmStr()); ExeTm.Tick();
}
printf("LogLike afterm warm-up: %f\n", LogLike());
CalcApxGraphLL(); // re-calculate LL (due to numerical errors)
CalcApxGraphDLL();
EstLLV.Add(TFltPr(WarmUp, LogLike));
if (TrueLL != -1) { TrueLLV.Add(TFltPr(WarmUp, TrueLL)); }
printf(" recalculated: %f\n", LogLike());
// start sampling
printf(" sampling (average per 1000 samples)\n");
TVec<TFltV> SamplVV(5);
for (int s = 0; s < NSamples; s++) {
if (SampleNextPerm(NId1, NId2)) { // new permutation
UpdateGraphDLL(NId1, NId2); NAccept++; }
for (int m = 0; m < AvgGradV.Len(); m++) { AvgGradV[m] += GradV[m]; }
AvgLL += GetLL();
SampleLLV.Add(GetLL());
/*SamplVV[0].Add(GetLL()); // gives worse autocoreelation than the avg below
SamplVV[1].Add(GradV[0]);
SamplVV[2].Add(GradV[1]);
SamplVV[3].Add(GradV[2]);
SamplVV[4].Add(GradV[3]);*/
if (s > 0 && s % 1000 == 0) {
printf(".");
for (int g = 0; g < AvgGradV.Len(); g++) {
GradVV[g].Add(TFltPr(WarmUp+s, AvgGradV[g] / 1000.0)); }
EstLLV.Add(TFltPr(WarmUp+s, AvgLL / 1000.0));
if (TrueLL != -1) { TrueLLV.Add(TFltPr(WarmUp+s, TrueLL)); }
AcceptV.Add(TFltPr(WarmUp+s, NAccept/1000.0));
// better (faster decaying) autocorrelation when one takes avg. of 1000 consecutive samples
/*SamplVV[0].Add(AvgLL);
SamplVV[1].Add(AvgGradV[0]);
SamplVV[2].Add(AvgGradV[1]);
SamplVV[3].Add(AvgGradV[2]);
SamplVV[4].Add(AvgGradV[3]); //*/
if (s % 100000 == 0 && DoPlot) {
const TStr Desc = TStr::Fmt("P(NodeSwap)=%g. Nodes: %d, Edges: %d, Params: %d, WarmUp: %s, Samples: %s", PermSwapNodeProb(),
Graph->GetNodes(), Graph->GetEdges(), GetParams(), TInt::GetMegaStr(WarmUp).CStr(), TInt::GetMegaStr(NSamples).CStr());
PlotGrad(EstLLV, TrueLLV, GradVV, AcceptV, OutFNm, Desc);
for (int n = 0; n < SamplVV.Len(); n++) {
PlotAutoCorrelation(SamplVV[n], 1000, TStr::Fmt("%s-n%d", OutFNm.CStr(), n), Desc); }
printf(" samples: %d, time: %s, samples/s: %.1f\n", s, ExeTm.GetTmStr(), double(s+1)/ExeTm.GetSecs());
}
AvgLL = 0; AvgGradV.PutAll(0); NAccept=0;
}
}
if (DoPlot) {
const TStr Desc = TStr::Fmt("P(NodeSwap)=%g. Nodes: %d, Edges: %d, Params: %d, WarmUp: %s, Samples: %s", PermSwapNodeProb(),
Graph->GetNodes(), Graph->GetEdges(), GetParams(), TInt::GetMegaStr(WarmUp).CStr(), TInt::GetMegaStr(NSamples).CStr());
PlotGrad(EstLLV, TrueLLV, GradVV, AcceptV, OutFNm, Desc);
for (int n = 0; n < SamplVV.Len(); n++) {
PlotAutoCorrelation(SamplVV[n], 1000, TStr::Fmt("%s-n%d", OutFNm.CStr(), n), Desc); }
}
return SampleLLV; // seems to work better for potential scale reduction plot
}

| void TKroneckerLL::UpdateGraphDLL | ( | const int & | SwapNId1, |
| const int & | SwapNId2 | ||
| ) |
Definition at line 1241 of file kronecker.cpp.
References TKronMtx::GetApxNoEdgeDLL(), TKronMtx::GetEdgeDLL(), GradV, Graph, TNGraph::IsEdge(), KronIters, TKronMtx::Len(), LLMtx, NodeDLLDelta(), NodePerm, and TVec< TVal, TSizeTy >::Swap().
Referenced by MetroGibbsSampleNext(), SampleGradient(), TestGradDescent(), and TestSamplePerm().
{
for (int ParamId = 0; ParamId < LLMtx.Len(); ParamId++) {
// permutation before the swap (swap back to previous position)
NodePerm.Swap(SwapNId1, SwapNId2);
// subtract old DLL
TFlt& DLL = GradV[ParamId];
DLL = DLL - NodeDLLDelta(ParamId, SwapNId1) - NodeDLLDelta(ParamId, SwapNId2);
// double-counted edges
const int PrevId1 = NodePerm[SwapNId1], PrevId2 = NodePerm[SwapNId2];
if (Graph->IsEdge(SwapNId1, SwapNId2)) {
DLL += - LLMtx.GetApxNoEdgeDLL(ParamId, PrevId1, PrevId2, KronIters)
+ LLMtx.GetEdgeDLL(ParamId, PrevId1, PrevId2, KronIters); }
if (Graph->IsEdge(SwapNId2, SwapNId1)) {
DLL += - LLMtx.GetApxNoEdgeDLL(ParamId, PrevId2, PrevId1, KronIters)
+ LLMtx.GetEdgeDLL(ParamId, PrevId2, PrevId1, KronIters); }
// permutation after the swap (restore the swap)
NodePerm.Swap(SwapNId1, SwapNId2);
// add new DLL
DLL = DLL + NodeDLLDelta(ParamId, SwapNId1) + NodeDLLDelta(ParamId, SwapNId2);
const int NewId1 = NodePerm[SwapNId1], NewId2 = NodePerm[SwapNId2];
// double-counted edges
if (Graph->IsEdge(SwapNId1, SwapNId2)) {
DLL += + LLMtx.GetApxNoEdgeDLL(ParamId, NewId1, NewId2, KronIters)
- LLMtx.GetEdgeDLL(ParamId, NewId1, NewId2, KronIters); }
if (Graph->IsEdge(SwapNId2, SwapNId1)) {
DLL += + LLMtx.GetApxNoEdgeDLL(ParamId, NewId2, NewId1, KronIters)
- LLMtx.GetEdgeDLL(ParamId, NewId2, NewId1, KronIters); }
}
}

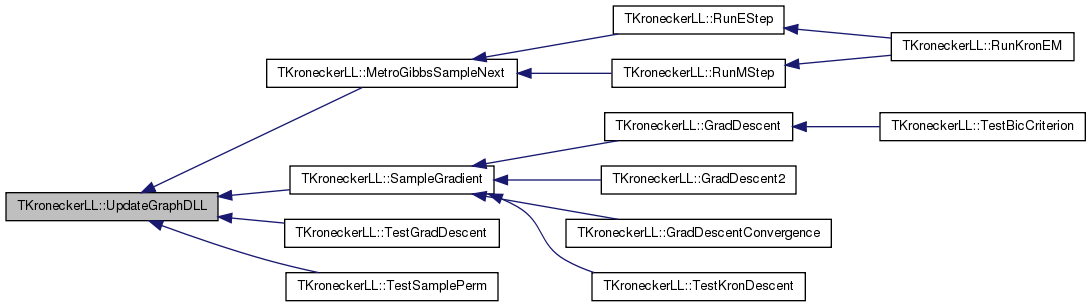
friend class TPt< TKroneckerLL > [friend] |
Definition at line 245 of file kronecker.h.
TCRef TKroneckerLL::CRef [private] |
Definition at line 119 of file kronecker.h.
TBool TKroneckerLL::DebugMode [private] |
Definition at line 141 of file kronecker.h.
Referenced by GradDescent(), RunKronEM(), and SetDebug().
TKronEMType TKroneckerLL::EMType [private] |
Definition at line 138 of file kronecker.h.
Referenced by MetroGibbsSampleSetup(), RunKronEM(), and SetRandomEdges().
TIntTrV TKroneckerLL::GEdgeV [private] |
Definition at line 125 of file kronecker.h.
Referenced by MetroGibbsSampleNext(), RestoreGraph(), SampleNextPerm(), SetGraph(), and SetRandomEdges().
TFltV TKroneckerLL::GradV [private] |
Definition at line 136 of file kronecker.h.
Referenced by CalcApxGraphDLL(), CalcFullApxGraphDLL(), CalcGraphDLL(), GetDLL(), GradDescentConvergence(), InitLL(), MetroGibbsSampleNext(), RunEStep(), RunMStep(), SampleGradient(), TestGradDescent(), TestKronDescent(), TestSamplePerm(), and UpdateGraphDLL().
PNGraph TKroneckerLL::Graph [private] |
Definition at line 120 of file kronecker.h.
Referenced by AppendIsoNodes(), CalcApxGraphDLL(), CalcApxGraphLL(), CalcFullApxGraphDLL(), CalcGraphDLL(), CalcGraphLL(), GetAbsErr(), GetGraph(), GradDescent(), GradDescent2(), GradDescentConvergence(), MetroGibbsSampleNext(), NodeDLLDelta(), NodeLLDelta(), RestoreGraph(), RunMStep(), SetBestDegPerm(), SetDegPerm(), SetGraph(), SetOrderPerm(), SetRandomEdges(), SetRndPerm(), SwapNodesLL(), TestGradDescent(), TestSamplePerm(), and UpdateGraphDLL().
TIntV TKroneckerLL::InvertPerm [private] |
Definition at line 129 of file kronecker.h.
Referenced by SampleNextPerm(), SetIPerm(), SetRandomEdges(), and SwapNodesLL().
TInt TKroneckerLL::KronIters [private] |
Definition at line 121 of file kronecker.h.
Referenced by AppendIsoNodes(), CalcApxGraphDLL(), CalcApxGraphLL(), CalcFullApxGraphDLL(), CalcGraphDLL(), CalcGraphLL(), GetAbsErr(), GetApxEmptyGraphDLL(), GetApxEmptyGraphLL(), GetEmptyGraphDLL(), GetEmptyGraphLL(), GetFullColLL(), GetFullGraphLL(), GetFullRowLL(), GetKronIters(), GradDescent(), GradDescent2(), GradDescentConvergence(), MetroGibbsSampleNext(), MetroGibbsSampleSetup(), NodeDLLDelta(), NodeLLDelta(), RunKronEM(), SetBestDegPerm(), SetGraph(), SetRandomEdges(), SwapNodesLL(), TestGradDescent(), and UpdateGraphDLL().
TIntTrV TKroneckerLL::LEdgeV [private] |
Definition at line 126 of file kronecker.h.
Referenced by MetroGibbsSampleNext(), RestoreGraph(), SetGraph(), and SetRandomEdges().
TKronMtx TKroneckerLL::LLMtx [private] |
Definition at line 134 of file kronecker.h.
Referenced by CalcApxGraphDLL(), CalcApxGraphLL(), CalcFullApxGraphDLL(), CalcGraphDLL(), CalcGraphLL(), GetEmptyGraphDLL(), GetEmptyGraphLL(), GetFullColLL(), GetFullGraphLL(), GetFullRowLL(), GetLLMtx(), GradDescent(), GradDescent2(), GradDescentConvergence(), InitLL(), MetroGibbsSampleNext(), NodeDLLDelta(), NodeLLDelta(), RunMStep(), SampleGradient(), SetGraph(), SwapNodesLL(), TestKronDescent(), and UpdateGraphDLL().
TFltV TKroneckerLL::LLV [private] |
Definition at line 142 of file kronecker.h.
Referenced by GetLLHist(), GradDescent(), RunKronEM(), and TestBicCriterion().
TFlt TKroneckerLL::LogLike [private] |
Definition at line 135 of file kronecker.h.
Referenced by CalcApxGraphLL(), CalcGraphLL(), GetLL(), GradDescentConvergence(), InitLL(), MetroGibbsSampleNext(), RunEStep(), RunMStep(), SampleNextPerm(), SwapNodesLL(), TestKronDescent(), and TestSamplePerm().
TInt TKroneckerLL::LSelfEdge [private] |
Definition at line 127 of file kronecker.h.
Referenced by MetroGibbsSampleNext(), RestoreGraph(), SetGraph(), and SetRandomEdges().
TInt TKroneckerLL::MissEdges [private] |
Definition at line 139 of file kronecker.h.
Referenced by MetroGibbsSampleSetup(), and RunKronEM().
TVec<TKronMtx> TKroneckerLL::MtxV [private] |
Definition at line 143 of file kronecker.h.
Referenced by GetParamHist(), GradDescent(), and RunKronEM().
TIntV TKroneckerLL::NodePerm [private] |
Definition at line 128 of file kronecker.h.
Referenced by CalcApxGraphDLL(), CalcApxGraphLL(), CalcFullApxGraphDLL(), CalcGraphDLL(), CalcGraphLL(), GetEmptyGraphDLL(), GetPermV(), NodeDLLDelta(), NodeLLDelta(), SampleNextPerm(), SetBestDegPerm(), SetDegPerm(), SetOrderPerm(), SetPerm(), SetRndPerm(), SwapNodesLL(), TestSamplePerm(), TKroneckerLL(), and UpdateGraphDLL().
TInt TKroneckerLL::Nodes [private] |
Definition at line 121 of file kronecker.h.
Referenced by AppendIsoNodes(), CalcApxGraphDLL(), CalcApxGraphLL(), CalcFullApxGraphDLL(), CalcGraphDLL(), CalcGraphLL(), GetEmptyGraphDLL(), GetNodes(), MetroGibbsSampleSetup(), SampleNextPerm(), SetBestDegPerm(), SetGraph(), SetOrderPerm(), SetRandomEdges(), and SetRndPerm().
TFlt TKroneckerLL::PermSwapNodeProb [private] |
Definition at line 123 of file kronecker.h.
Referenced by SampleNextPerm(), and TestSamplePerm().
TKronMtx TKroneckerLL::ProbMtx [private] |
Definition at line 134 of file kronecker.h.
Referenced by AppendIsoNodes(), GetAbsErr(), GetApxEmptyGraphDLL(), GetApxEmptyGraphLL(), GetDim(), GetParams(), GetProbMtx(), GradDescent(), GradDescent2(), GradDescentConvergence(), InitLL(), MetroGibbsSampleSetup(), RunKronEM(), RunMStep(), SetBestDegPerm(), SetGraph(), SetRandomEdges(), TestKronDescent(), and TestSamplePerm().
TInt TKroneckerLL::RealEdges [private] |
Definition at line 132 of file kronecker.h.
Referenced by RunKronEM(), RunMStep(), and SetGraph().
TInt TKroneckerLL::RealNodes [private] |
Definition at line 131 of file kronecker.h.
Referenced by IsObsEdge(), IsObsNode(), MetroGibbsSampleSetup(), RestoreGraph(), RunKronEM(), RunMStep(), and SetGraph().